题目内容
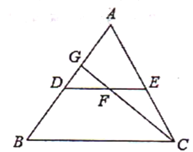
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
A.4cm2 B.6cm2 C.8cm2 D.9cm2
【答案】A
【解析】
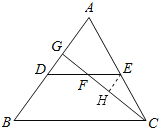
试题分析:取CG的中点H,连接EH,根据三角形的中位线定理可得EH∥AD,再根据两直线平行,内错角相等可得∠GDF=∠HEF,然后利用“角边角”证明△DFG和△EFH全等,根据全等三角形对应边相等可得FG=FH,全等三角形的面积相等可得S△EFH=S△DGF,再求出FC=3FH,再根据等高的三角形的面积比等于底边的比求出两三角形的面积的比,从而得解.
解:如图,取CG的中点H,连接EH,
∵E是AC的中点,
∴EH是△ACG的中位线,
∴EH∥AD,
∴∠GDF=∠HEF,
∵F是DE的中点,
∴DF=EF,
在△DFG和△EFH中,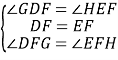 ,
,
∴△DFG≌△EFH(ASA),
∴FG=FH,S△EFH=S△DGF,
又∵FC=FH+HC=FH+GH=FH+FG+FH=3FH,
∴S△CEF=3S△EFH,
∴S△CEF=3S△DGF,
∴S△DGF=![]() ×12=4(cm2).
×12=4(cm2).
故选:A.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目