ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŅŃÖŖ£ŗ”÷ABCŌŚ×ų±źĘ½ĆęÄŚ£¬Čżøö¶„µćµÄ×ų±źĪŖA(0£¬3)”¢B(3£¬4)”¢C(2£¬2)£¬(Õż·½ŠĪĶųøńÖŠ£¬ĆæøöŠ”Õż·½ŠĪ±ß³¤ĪŖ1øöµ„Ī»³¤¶Č)
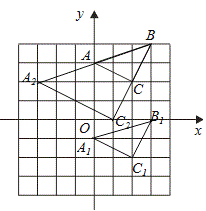
£Ø1£©»³ö”÷ABCĻņĻĀĘ½ŅĘ4øöµ„Ī»µĆµ½µÄ”÷A1B1C1£»
£Ø2£©ŅŌBĪŖĪ»ĖĘÖŠŠÄ£¬ŌŚĶųøńÖŠ»³ö”÷A2BC2£¬Ź¹”÷A2BC2Óė”÷ABCĪ»ĖĘ£¬ĒŅĪ»ĖʱČ2”Ć1£¬Ö±½ÓŠ“³öC2µć×ų±źŹĒ £»
£Ø3£©”÷A2BC2µÄĆ껿ŹĒ Ę½·½µ„Ī»£®

”¾“š°ø”æ£Ø1£©»Ķ¼¼ū½āĪö£»£Ø2£© »Ķ¼¼ū½āĪö£¬ (1£¬0)£»£Ø3£© 10£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĶųøń½į¹¹£¬ÕŅ³öµćA”¢B”¢CĻņĻĀĘ½ŅĘ4øöµ„Ī»µÄ¶ŌÓ¦µćA1”¢B1”¢C1µÄĪ»ÖĆ£¬Č»ŗóĖ³“ĪĮ¬½Ó¼“æÉ£»£Ø2£©ŃÓ³¤BAµ½A2£¬Ź¹AA2=AB£¬ŃÓ³¤BCµ½C2£¬Ź¹CC2=BC£¬Č»ŗóĮ¬½ÓA2C2¼“æÉ£¬ŌŁøł¾ŻĘ½ĆęÖ±½Ē×ų±źĻµŠ“³öC2µćµÄ×ų±ź£»£Ø3£©ĄūÓĆ”÷A2BC2ĖłŌŚµÄ¾ŲŠĪµÄĆ껿¼õČ„ĖÄÖÜČżøöŠ”Ö±½ĒČż½ĒŠĪµÄĆ껿£¬ĮŠŹ½¼ĘĖć¼“æɵĆ.
ŹŌĢā½āĪö£ŗ
£Ø1£©ČēĶ¼ĖłŹ¾£ŗ
£Ø2£©ČēĶ¼ĖłŹ¾£ŗ
C2µć×ų±źŹĒ(1£¬0)£»
£Ø3£©”÷A2BC2µÄĆ껿ŹĒ=6”Į4£![]() ”Į2”Į6£
”Į2”Į6£![]() ”Į2”Į4£
”Į2”Į4£![]() ”Į2”Į4 =10Ę½·½µ„Ī»£®
”Į2”Į4 =10Ę½·½µ„Ī»£®

 ¼ā×ÓÉśŠĀæĪĢĆæĪŹ±×÷ŅµĻµĮŠ“š°ø
¼ā×ÓÉśŠĀæĪĢĆæĪŹ±×÷ŅµĻµĮŠ“š°ø