题目内容
如图，在□ABCD中，∠ABC的平分线交AD于点E，且AE－DE＝1，若□ABCD的周长为22，则AB的长为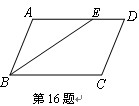 
4
设AE=x则DE=x-1，由?ABCD和∠ABC的平分线，推出∠AEB=∠ABE=∠CBE，得出AB=AE，再根据?ABCD的周长为22，列出方程即可求出答案．
解：设AE=x则DE=x-1，
∵四边形ABCD是平行四边形，
∴AD=CB，AB=DC，AD∥BC，
∴∠CBE=∠AEB，
∵BE平分∠ABC，
∴∠CBE=∠ABE，
∴∠AEB=∠ABE，
∴AB=AE=x，
∵?ABCD的周长为22，
∴2x+2（x+x-1）=22，
解得：x=4，
故答案为：4．
解：设AE=x则DE=x-1，
∵四边形ABCD是平行四边形，
∴AD=CB，AB=DC，AD∥BC，
∴∠CBE=∠AEB，
∵BE平分∠ABC，
∴∠CBE=∠ABE，
∴∠AEB=∠ABE，
∴AB=AE=x，
∵?ABCD的周长为22，
∴2x+2（x+x-1）=22，
解得：x=4，
故答案为：4．
练习册系列答案
相关题目
处，连结BE．
是菱形；
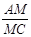的值是 ▲ . 
，则菱形ABCD的周长是________．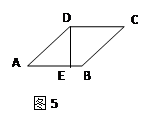
、
的正方形纸片和
的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．
