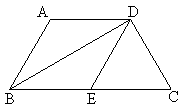
题目内容
菱形ABCD边长为4，点E在直线AD上，DE=3，联结BE与对角线AC交点M，那么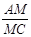
的值是 ▲ .
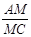的值是 ▲ . 
或
根据菱形的性质，可得对边平行，即可得到△AOE∽△COB，注意作图时需要分析点E在线段AD上还是在线段AD的延长线上．
解：①如图：
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AOE∽△COB，
∴
，
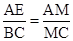∵DE=3，
∴AE=AD-DE=1，
∴
=
，
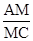②如图：
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AOE∽△COB，
∴，
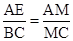∵DE=3，
∴AE=AD+DE=7，
∴=
，
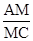故答案为：或．
解：①如图：
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AOE∽△COB，
∴
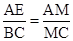，∵DE=3，
∴AE=AD-DE=1，
∴
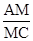=，②如图：
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AOE∽△COB，
∴
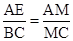，∵DE=3，
∴AE=AD+DE=7，
∴
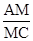=，故答案为：
或．
练习册系列答案
相关题目
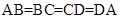，对角线AC与BD相交于点O．若不增加任何字母与辅助线，要使得四边形ABCD是正方形，则还需增加的一个条件是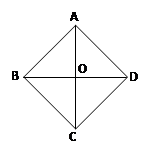
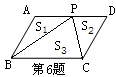
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
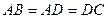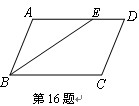
＝4，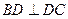
，E为BC中点，连结DE. 
