题目内容
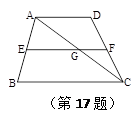
如图,在梯形ABCD中,AD∥BC,AB="DC" ,过点D作DE∥AB 交BC于点E.

(1) 请你判断四边形ABED的形状,并说明理由;
(2) 当△DEC为等边三角形时,
① 求∠B的度数;
② 若AD=4,DC=3,求等腰梯形ABCD的周长.

(1) 请你判断四边形ABED的形状,并说明理由;
(2) 当△DEC为等边三角形时,
① 求∠B的度数;
② 若AD=4,DC=3,求等腰梯形ABCD的周长.
(1)平行四边形
(2)
① 60°
② 17
(1) 四边形ABED是平行四边形;………………1分
理由如下:
∵AD∥BC,AB="DC" ,DE∥AB
∴四边形ABED是平行四边形. ………………2分
(2) ① ∵△DEC为等边三角形
∴∠C=60°, ………………3分
在梯形ABCD中,AD∥BC,AB="DC" ,
∴∠B=∠C=60°. ………………5分
② ∵四边形ABED是平行四边形
∴BE=AD=4, ………………6分
∵△DEC为等边三角形,
∴CE=DC=3, ………………7分
∵AB=DC
∴等腰梯形ABCD的周长=AB+(BE+EC)+DC+AD=3+(4+3)+3+4="17." ………8分
理由如下:
∵AD∥BC,AB="DC" ,DE∥AB
∴四边形ABED是平行四边形. ………………2分
(2) ① ∵△DEC为等边三角形
∴∠C=60°, ………………3分
在梯形ABCD中,AD∥BC,AB="DC" ,
∴∠B=∠C=60°. ………………5分
② ∵四边形ABED是平行四边形
∴BE=AD=4, ………………6分
∵△DEC为等边三角形,
∴CE=DC=3, ………………7分
∵AB=DC
∴等腰梯形ABCD的周长=AB+(BE+EC)+DC+AD=3+(4+3)+3+4="17." ………8分

练习册系列答案
相关题目
 ,这个正方形原来的边长是( )
,这个正方形原来的边长是( )
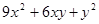 (
( ,
, ),利用分解因式,写出表示该正方形的边长的代数式
),利用分解因式,写出表示该正方形的边长的代数式 
 A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2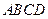 的对角线
的对角线 和
和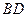 相交于点
相交于点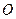 ,
,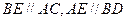 ,试判断四边形
,试判断四边形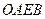 的形状,并说明理由.
的形状,并说明理由.
 ,求原铁皮的长
,求原铁皮的长