题目内容
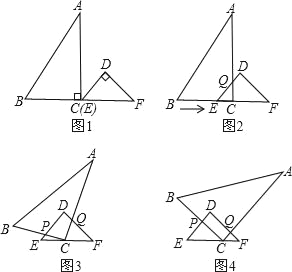
【题目】如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
(1)用含有x的代数式表示CE的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.

【答案】①CE=6x;②x=![]() ;③见解析.
;③见解析.
【解析】
(1)首先证明△ABC∽△DBP∽△FEC,即可得出比例式进而得出表示CE的长;
(2)根据当点F与点B重合时,FC=BC,即可得出答案;
(3)首先证明Rt△DOE∽Rt△CEF,得出![]() 即可得出y与x之间的函数关系式.
即可得出y与x之间的函数关系式.
(1)∵∠C=90°,PD⊥BC,
∴DP∥AC,
∴△DBP∽△ABC,四边形PDEC为矩形,
∴![]() ,CE=PD.
,CE=PD.
∴PD=![]() =6x.
=6x.
∴CE=6x;
(2)∵∠CEF=∠ABC,∠C为公共角,
∴△CEF∽△CBA,
∴![]() .
.
∴CF=![]() =9x.
=9x.
当点F与点B重合时,CF=CB,9x=20.
解得x=![]() .
.
(3)当点F与点P重合时,BP+CF=CB,4x+9x=20,
解得x=![]() .
.
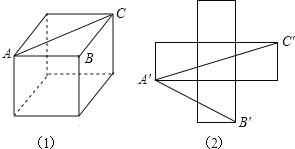
当0<x<![]() 时,如图①,
时,如图①,
y=![]() =-51x2+120x.
=-51x2+120x.
当![]() ≤x≤
≤x≤![]() 时,如图②,
时,如图②,
y=![]() DE×DG=
DE×DG=![]() (204x)
(204x)![]() (204x)=
(204x)=![]() (20-4x)2.
(20-4x)2.
(或y=![]() x2
x2![]() x+
x+![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4