Question

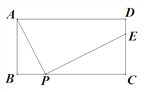
【题目】如图，矩形ABCD中，AB＝4，BC＝（）.P为边BC上一动点（不与B、C重合），过P点作PE⊥AP交直线CD于E.

（1）求证：△ABP∽△PCE；

（2）当P为BC中点时，E恰好为CD的中点，求的值；

（3）若=12,DE=1,求BP的长.

Answer 1

【答案】（1）证明见解析；（2）；（3），，2，10

【解析】试题分析：（1）由四边形ABCD是矩形可得∠B=∠C=90°，由PE⊥AP得∠P=∠PEC,从而可证△ABP∽△PCE；

（2）由△ABP∽△PCE可求出m的值.

（3）由△ABP∽△PCE可求出BP的长.

试题解析：（1）∵四边形ABCD是矩形

∴∠B=∠C=90°

∵PE⊥AP

∴∠APB+∠CPE=90°

∵∠CPE+∠CEP=90°

∴∠APB=∠CEP

∴△ABP∽△PCE

（2）∵P为BC中点时，E为CD的中点,且BC=m,CD=4

∴BP=CP=,CE=2

∵△ABP∽△PCE

∴ 即：

∴m=

即m的值为

（3）设BP的长为x，

∵△ABP∽△PCE，

∴

∴或，

解得x1= ，x2=， x3=2， x4=10

∴BP的长为，，2，10