题目内容
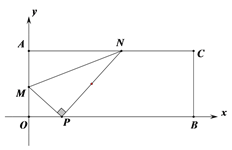
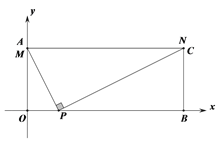
【题目】如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于______________。
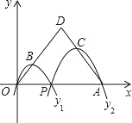
【答案】4
【解析】过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,则BF+CM是这两个二次函数的最大值之和,BF∥DE∥CM,求出AE=OE=2,DE=4,设P(3x,0),根据二次函数的对称性得出OF=PF=x,推出△OBF∽△ODE,△ACM∽△ADE,得出![]() ,
,![]() ,,代入求出BF和CM,相加即可求出答案.
,,代入求出BF和CM,相加即可求出答案.
解:过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,
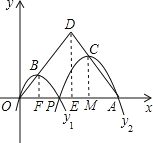
∵BF⊥OA,DE⊥OA,CM⊥OA,
∴BF∥DE∥CM,
∵OD=AD=5,DE⊥OA,
∴OE=EA=![]() OA=3,
OA=3,
由勾股定理得:DE=![]() =4,
=4,
设P(3x,0),根据二次函数的对称性得出OF=PF=x,
∵BF∥DE∥CM,
∴△OBF∽△ODE,△ACM∽△ADE,
∴![]() ,
,![]() ,
,
∵AM=PM=![]() (OA-OP)=
(OA-OP)=![]() (6-2x)=3-x,
(6-2x)=3-x,
即![]() ,
,![]() ,
,
解得:BF=![]() ,CM=
,CM=![]()
∴BF+CM=![]() +
+![]() =4.
=4.
故答案为:4.
“点睛”此题考查了二次函数的最值,勾股定理,等腰三角形的性质,以及相似三角形的性质和判定的应用,题目比较好,但是有一定的难度,属于综合性试题.

练习册系列答案
相关题目