题目内容
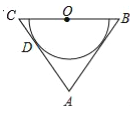
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据锐角三角函数,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
试题解析:(1)证明:如图1,
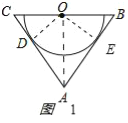
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=![]() ,AB=12,得OB=8.
,AB=12,得OB=8.
由勾股定理,得AO=4![]() .
.
由三角形的面积,得S△AOB=![]() ABOE=
ABOE=![]() OBAO,
OBAO,
∴OE=![]() =
=![]() ,
,
即半圆O所在圆的半径是![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目