题目内容
【题目】已知：如图，梯形ABCD中，AD∥BC，∠B=90°，AD=AB=4，BC=7，点E在BC边上，将△CDE沿DE折叠，点C恰好落在AB边上的点C'处．
（1）求∠C'DE的度数；
（2）求△C'DE的面积．
【答案】（1）45°；（2）
．
【解析】
（1）首先作DF⊥BC于F，根据已知证出△AC′D≌△FCD，再求出∠C′DE=∠CDE，即可得出答案；（2）根据EC=x，则BE=7-x，C′E=x，再根据勾股定理求出EC的长，即可求出△C′DE的面积．
（1）过点D作DF⊥BC于F
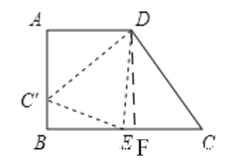
∵AD∥BC，∠B=90°，AD=AB，
∴四边形ABFD是正方形．
∴DF=BF=AB=4，FC=3，
在Rt△DFC中，
,
∴C′D=5，
∵AD=FD，∠A=∠DFC=90°，C′D=CD，
∴△AC′D≌△FCD，
∴∠ADC′=∠FDC，AC′=FC=3，
∴∠ADF=∠ADC′+∠C′DF=∠FDC+∠C′DF=∠C′DC=90°，
∵∠C′DE=∠CDE，
∴∠C′DE=45°；
（2）设EC=x，则BE=7-x，C′E=x，
∵AC′=3，
∴BC'=1，
在Rt△BEC′中（7-x）2+1=x2
解方程，得：
，
∴
.
练习册系列答案
相关题目
【题目】去年6月某日自治区部分市、县的最高气温（℃）如下表：
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温（℃） | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是（ ）
A.32，32
B.32，30
C.30，30
D.30，32
