题目内容
【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0) 
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
【答案】
(1)解:把点A(2,0)、B(﹣4,0)的坐标代入y=﹣x2+2bx+c得, ![]() ,
,
∴b=﹣1.c=8,
∴抛物线的解析式为y=﹣x2﹣2x+8
(2)解:如图1,

设抛物线的对称轴与x轴的交点为H,把点A(2,0)的坐标代入y=﹣x2+2bx+c得,
﹣4+4b+c=0①,
∵抛物线的顶点为P,
∴y=﹣x2+2bx+c=﹣(x﹣b)2+b2+c,
∴P(b,b2+c),
∴PH=b2+c,AH=2﹣b,
在Rt△PHA中,tan∠OAP= ![]() ,
,
∴ ![]() =3②,
=3②,
联立①②得,  ,
,
∴ ![]() (不符合题意,舍)或
(不符合题意,舍)或 ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+8
(3)解:∵如图2,
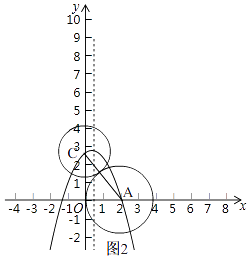
抛物线y=﹣x2+2bx+c与y轴正半轴交于点C,
∴C(0,c)(c>0),
∴ ![]() OC=
OC= ![]() c,
c,
∵A(2,0),
∴OA=2,
∴AC= ![]() ,
,
∵⊙A与⊙C外切,
∴AC= ![]() c+2=
c+2= ![]() ,
,
∴c=0(舍)或c= ![]() ,
,
把点A(2,0)的坐标代入y=﹣x2+2bx+c得,﹣4+4b+c=0,
∴b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+
x+ ![]() .
.
【解析】(1)利用待定系数法即可确定出函数解析式;(2)用tan∠OAP=3建立一个b,c的关系,再结合点A得出的等式即可求出b,c进而得出函数关系式;(3)用两圆外切,半径之和等于AC建立方程结合点A代入建立的方程即可得出抛物线解析式.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案