题目内容
【题目】(1)尝试探究
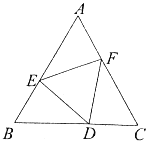
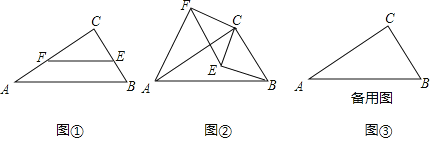
如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
①![]() 的值为多少;②直线
的值为多少;②直线![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)类比延伸
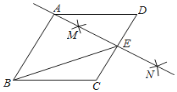
如图②,若将图①中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,
,![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)拓展运用
若![]() ,
,![]() ,在旋转过程中,当
,在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;
;![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]()
【解析】
(1)①利用三角函数可求出CF=![]() EC,AC=
EC,AC=![]() BC,再通过线段的差进行转化可得出AF=
BC,再通过线段的差进行转化可得出AF=![]() BE,即可得出答案;②根据
BE,即可得出答案;②根据![]() ,即可得出直线
,即可得出直线![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)先利用三角函数求出CF与EC,AC与BC的关系,再证出![]() ∽
∽![]() ,利用相似的性质即可得出答案;
,利用相似的性质即可得出答案;
(3)根据题意可画出两种满足题意的图形,再利用(2)中的结论即可求出答案.
解:(1)①∵在△ABC中,∠ACB=90°,∠A=30°,EF//AB,
∴∠CFE=∠A=30°,
∴CF=![]() EC,AC=
EC,AC=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC- ![]() EC=
EC=![]() (BC-EC)=
(BC-EC)= ![]() BE,
BE,
∴![]() =
=![]() ,
,
②∵![]() ,
,
∴AF⊥BE;
(2)![]() ;
;![]()
理由如下:由(1)及旋转的性质知,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ;
;
![]() ,
,
又![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() .
.
如图,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
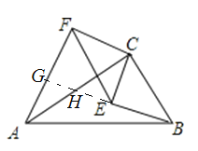
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
即![]() ;
;
(3)![]() 或
或![]()

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目