题目内容
【题目】解方程与方程组
(1)解方程:x2﹣6x﹣6=0;
(2)解不等式组:  .
.
【答案】
(1)解:a=1,b=﹣6,c=﹣6,
则△=b2﹣4ac=36+24=40>0,
则x= ![]() =3±
=3± ![]() ,
,
则x1=3+ ![]() ,x2=3﹣
,x2=3﹣ ![]() ;
;
(2)解: 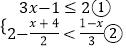 ,
,
解①得:x≤1,
解②得:x>﹣2,
则不等式组的解集是:﹣2<x≤1.
【解析】(1)利用求根公式即可直接求解;(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【考点精析】本题主要考查了一元一次不等式组的解法的相关知识点,需要掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.

 全程金卷系列答案
全程金卷系列答案【题目】某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )
人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
金额(元) | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
A.极差是195000
B.中位数是15000
C.众数是15000
D.平均数是15000
【题目】文昌某校准备组织学生及学生家长到三亚进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上;根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元;已知学生家长与教师的人数之比为2:1,文昌到三亚的火车票价格(部分)如下表所示:
运行区间 | 公布票价 | 学生票 | ||
上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
文昌 | 三亚 | 81(元) | 68(元) | 51(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?