题目内容
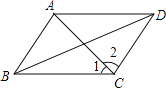
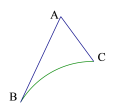
【题目】如图所示,AB=6,AC=3,∠BAC=60°,![]() 为⊙O上的一段弧,且∠BOC=60°,分别在
为⊙O上的一段弧,且∠BOC=60°,分别在![]() 、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
【答案】![]()
【解析】
连接AP、O、OA,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点M,P关于AC的对称点N,连接MN,交AB于点E,交AC于点F,连接PE、PF,所以
AM=AP=AN,设AP=r,则MN=![]() ,所以PE+EF+PF=ME+EF+FN=MN=
,所以PE+EF+PF=ME+EF+FN=MN=![]() ,即当AP最小时,PE+EF+PF可取最小值,由AP+OP≥OA可知AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,利用勾股定理即可求得AP的长度,即可解答.
,即当AP最小时,PE+EF+PF可取最小值,由AP+OP≥OA可知AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,利用勾股定理即可求得AP的长度,即可解答.
连接BC,取AB的中点D,连接CD,如图1

则AD=BD=3
∴AD=BD=AC
∵∠BOC=60°
∴△ADC是等边三角形
∴CD=AC=3
∴CD=![]() AB
AB
∴∠ACB=90°
连接AP、O、OA,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点M,P关于AC的对称点N,连接MN,交AB于点E,交AC于点F,连接PE、PF,

∴AM=AP=AN
∵∠MAB=∠PAB,∠NAC=∠PAC
∵∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°
∴∠MAN=120°
∴M、P、N在以A为圆心AP为半径的圆上
设AP=r,则MN=![]()
∵PE=ME,PF=FN
∴PE+EF+PF=ME+EF+FN=MN=![]()
∴当AP最小时,PE+EF+PF可取最小值
∵AP+OP≥OA
∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值
在Rt△ABC中,∵AB=6,AC=3,∠BAC=60°
∴BC=![]()
∵∠BOC=60°,OB=OC
∴△OBC是等边三角形
∴OC=BC=![]() ,作OH⊥AC交AC的延长线于H
,作OH⊥AC交AC的延长线于H
在Rt△OCH中,∵OC=![]() ,∠OCH=30°
,∠OCH=30°
∴OH=![]() OC=
OC=![]() ,CH=
,CH=![]() OH=
OH=![]()
在Rt△AOH中,AO=![]()
此时AP=r=![]()
∴PE+EF+PF的最小值为![]()
故答案为:![]()

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案