��Ŀ����
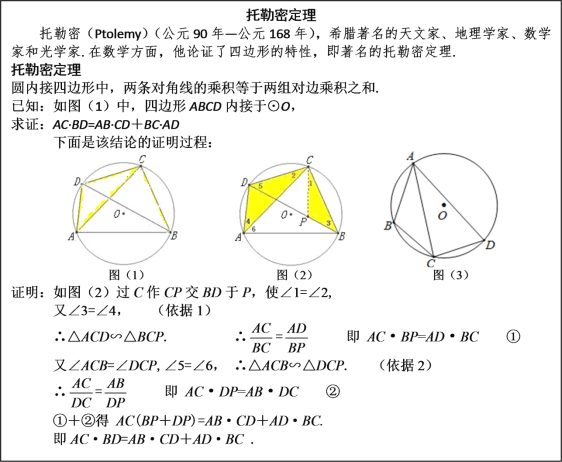
����Ŀ���ڡ�ABC�У�AB��BC��2![]() ����ABC��120�㣬��CDEΪ�ȱ������Σ�CD��2������AD��MΪAD�е㣮
����ABC��120�㣬��CDEΪ�ȱ������Σ�CD��2������AD��MΪAD�е㣮
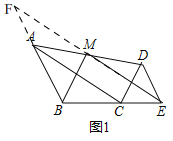
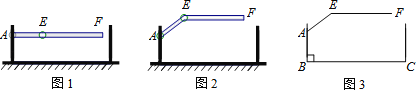
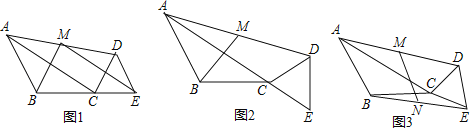
��1����ͼ1����B��C��E���㹲��ʱ���뻭����EDM���ڵ�M�����ĶԳ�ͼ�Σ���֤��BM��ME��
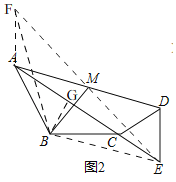
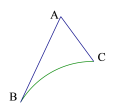
��2����ͼ2����A��C��E���㹲��ʱ����BM�ij���
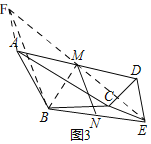
��3����ͼ3��ȡBE�е�N����MN������CDE�Ƶ�C��ת��ֱ��д����ת�������߶�MN��ȡֵ��Χ��_____��
���𰸡���1���𰸼���������2��![]() ����3��
����3��![]() ��
��
��������
��1��������ͼ�Σ�����֤����AMF�ա�DME�����ɵó����ۣ�
��2��ͬ��1���ķ����ó���AMF�ա�DMF�������ı��ε��ڽǺͶ�����ƽ�ǵĶ���ó���BCE����BAF���ɵó���BME��90�㣬����ù��ɶ������ɵó����ۣ�
��3��ͬ��2���ķ����ó���BME��90�㣬�����ó�BE��2MN������������ε����߹�ϵ���ɵó����ۣ�
�⣺��1��֤������ͼ1��
�ӳ�BA��EM���ڵ�F��������FAM��Ϊ����
�ߡ�CDE�ǵȱ������Σ�
��CD��CE��DE����CED��60�㣬
�ߡ�ABC��120�㣬
���ABC+��CED��180�㣬
��B��C��E���㹲�ߣ�
��AB��DE��
���FAM����MDE����MED����F��
�ߵ�M��AD�е㣬
��AM��DM��
���AMF�ա�DME��
��AF��DE��CE��FM��ME��
��AB��BC��
��BF��BE��
��BM��ME��
��2��֤������ͼ2���ӳ�EM����F��ʹMF��ME������BF��AF��BE��
��AM��DM����FMA����DME��
���AMF�ա�DMF��
��AF��DE��CE����FAD����ADE��
���ı���BADE�У��ߡ�BAD+��ADE+��DEB+��EBA��360�㣬
�ߡ�ABC��120�㣬��CED��60�㣬
���CBE+��CEB+��BAD+��ADE��180�㣬
�ߡ�CBE+��CEB+��BCE��180�㣬
���BCE����BAD+��ADE��
���BCE����BAF��
��AB��AC��
���AFB�ա�CEB��
��BF��BE����ABF����CBE��
���FBE����ABC��120�㣬��BEF��30�㣬
���BME��90�㣬BE��2BM��
�ڡ�ABC�У�AB��AC��2![]() ����ABC��120�㣬���BAC��30�㣬
����ABC��120�㣬���BAC��30�㣬
����B��BG��AC��G��
��BG��![]() ��CG��AG��3��
��CG��AG��3��
��EG��CG+CE��3+2��5
��Rt��BCE�У����ݹ��ɶ����ã�BE��2![]() ��
��
��BM��![]() ��
��
��3����ͼ3���ӳ�EM����F��ʹMF��ME������BF��AF��BM��
��AM��DM����FMA����DME��
���AMF�ա�DME��
��AF��DE��CE����FAD����ADE��
���ı���BADE�У��ߡ�BAD+��ADE+��DEB+��EBA��360�㣬
�ߡ�ABC��120�㣬��CED��60�㣬
���CBE+��CEB+��BAD+��ADE��180�㣬
�ߡ�CBE+��CEB+��BCE��180�㣬
���BCE����BAD+��ADE��
���BCE����BAF��
��AB��CB��
���AFB�ա�CEB��
��BF��BE����ABF����CBE��
���FBE����ABC��120�㣬��BEF��30�㣬
���BME��90�㣬
�ߵ�N��BE���е㣬
��MN��![]() BE��
BE��
����BE��2MN��
�ڡ�BCE�У�BC��2![]() ��CE��CD��2��
��CE��CD��2��
��2![]() ��2��BE��2
��2��BE��2![]() +2��
+2��
��2![]() ��2��2MN��2
��2��2MN��2![]() +2��
+2��
����![]() ��1��MN��
��1��MN��![]() +1��
+1��
�ʴ�Ϊ��![]() ��1��MN��
��1��MN��![]() +1��
+1��