Question

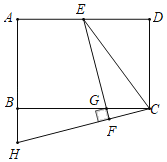
【题目】如图，在长方形ABCD中，点E是AD的中点，连接CE，将△CDE沿着CE翻折得到△CFE，EF交BC于点G，CF的延长线交AB的延长线于点H，若AH＝25，BC＝40，则FG＝_____．

Answer 1

【答案】.

【解析】

由矩形的性质得出∠A＝∠D＝90°，AD＝BC＝40，由点E是AD的中点，得出AE＝DE＝AD＝20，由折叠性质得FE＝DE＝20，∠EFC＝∠D＝90°，CF＝CD，∠CEF＝∠CED，则AE＝EF，∠EFH＝90°＝∠A，连接EH，由HL证得Rt△AEH≌Rt△FEH，得出FH＝AH＝25，∠AEH＝∠FEH，推出∠HEC＝90°，设CD＝x，则CH＝25+x，由勾股定理得出EH2＝AH2+AE2，CE2＝DE2+CD2，CH2＝E2+CE2，则CH2＝AH2+AE2+DE2+CD2，即（25+x）2＝252+202+202+x2，解得x＝16，作EM⊥BC于M，则EM＝CD＝CF＝16，CM＝DE＝20，由AAS证得△EMG≌△CFG，得出MG＝FG，设EG＝y，则MG＝FG＝20﹣y，在Rt△EMG中，由勾股定理得y2＝162+（20﹣y）2，解得y＝，即可得出结果．

解：∵四边形ABCD是矩形，

∴∠A＝∠D＝90°，AD＝BC＝40，

∵点E是AD的中点，

∴AE＝DE＝AD＝20，

由折叠性质得：FE＝DE＝20，∠EFC＝∠D＝90°，CF＝CD，∠CEF＝∠CED，

∴AE＝EF，∠EFH＝90°＝∠A，

连接EH，如图所示：

在Rt△AEH和Rt△FEH中，，

∴Rt△AEH≌Rt△FEH（HL），

∴FH＝AH＝25，∠AEH＝∠FEH，

∴∠HEC＝∠FEH+∠CEF＝∠AEF+∠DEF＝×180°＝90°，

设CD＝x，则CH＝25+x，

∵EH2＝AH2+AE2，CE2＝DE2+CD2，CH2＝HE2+CE2，

∴CH2＝AH2+AE2+DE2+CD2，

即（25+x）2＝252+202+202+x2，

整理得：50x＝800，

解得：x＝16，

作EM⊥BC于M，

则EM＝CD＝CF＝16，CM＝DE＝20，

在△EMG和△CFG中，，

∴△EMG≌△CFG（AAS），

∴MG＝FG，

设EG＝y，则MG＝FG＝20﹣y，

在Rt△EMG中，由勾股定理得：y2＝162+（20﹣y）2，

解得：y＝，

∴FG＝20﹣＝，

故答案为：．