Question

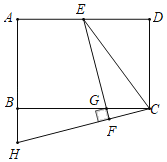
【题目】如图，在正方形中，、分别是边、上的点，且，与相交于点，则图中与相似的三角形有________．

Answer 1

【答案】，,

【解析】

利用正方形的性质，运用SAS证明△ABF≌△DAE，再由全等三角形的性质可得出答案．

∵四边形ABCD是正方形，
∴AB=AD，∠BAF=∠ADE=90°．
∵CE=DF，
∴AF=DE．
在△ABF与△DAE中，
∵ ，
∴△ABF≌△DAE（SAS）．
∴AE=BF；
∴∠AFB=∠AED．
∵∠AED+∠DAE=90°，
∴∠AFB+∠DAE=90°，
∴∠AOF=90°，即AE⊥BF．
∵∠BAF=90°，
∴∠AFB+∠ABF=90°．
∵∠ABF+∠BAM=90°，
∴∠BAM=∠AFM，
∴△ABM∽△FAM．
同理，△ABM∽△FBA．△ABM∽△AED
故答案为：△ABM∽△FAM，△ABM∽△FBA,△ABM∽△AED．