题目内容
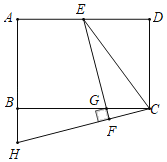
【题目】如图，梯形ABCD中，AD∥BC，CD⊥BC，已知AB=5，BC=6，cosB=
．点O为BC边上的动点，以O为圆心，BO为半径的⊙O交边AB于点P．
（1）设OB=x，BP=y，求y与x的函数关系式，并写出函数定义域；
（2）当⊙O与以点D为圆心，DC为半径⊙D外切时，求⊙O的半径；
（3）连接OD、AC，交于点E，当△CEO为等腰三角形时，求⊙O的半径．
【答案】（1）y=
x（0＜x≤
）；（2）1.8；（3）当△CEO为等腰三角形时，⊙O的半径为3或4．
【解析】
（1）首先作OM⊥BD，即可满足垂径定理，在直角△OBM中求得BM的长，即可求得BP；
（2）连接OD．作AN⊥BC，根据三角函数即可求得CD的长，根据两圆相外切时，圆心距等于半径的和即可得到一个关于半径长的一个方程，即可求得半径长；
（3）当△CEO为等腰三角形时，利用当EO=EC时，当CE=CO时，分别求得圆的半径．
（1）作OM⊥BP，
则BP=2BM．
在直角△BMO中，
cosB=
=
．
∴BM=OBcosB=．
则BP=2BM=．
∴函数的解析式是：y=x（0＜x≤）；
（2）连接OD．作AN⊥BC．
∵在直角△ABN中，cosB=
=．
∴BN=ABcosB=5×=3．
则AN=CD=4．
在直角△OCD中，OC=BC﹣OB=6﹣x，CD=4．
则OD=
．
当两圆相切时： =x+4
解得：x=1.8；
（3）在Rt△ACD中，AC=5，设⊙O的半径为x，
当EO=EC时，∠EOC=∠ACB，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠EOC，
∴AB∥OD，
又∵AD∥BC，
∴OB=AD=3，
∴⊙O的半径为3，
当OE=OC时，∠ECO=∠CEO，
∵AD∥BC，
∴∠DAE=∠ECO，
∵∠AED=∠CEO，∴∠DAE=∠AED，
∴AD=DE=3，
∴OD=OE+DE=6﹣x+3=9﹣x，
在Rt△OCD中，
∵CD2+OC2=OD2，
∴42+（6﹣x）2=（9﹣x）2，
解得：x=
（不合题意舍去）
当CE=CO时，∠CEO=∠COE，
∵AD∥BC，
∴∠ADE=∠COE，
∵∠AED=∠CEO，
∴∠AED=∠ADE，
∴AD=AE=3，
∵CE+AE=AC，
∴6﹣x+3=5，
∴x=4，
∴⊙O的半径为4．
综上所述，当△CEO为等腰三角形时，⊙O的半径为3或4．
