题目内容
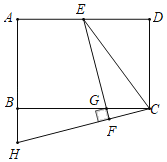
【题目】如图,AB为⊙O的直径,C为⊙O上弧BF的中点,CD⊥AF,垂足为D,AB、DC的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OC, 根据C为⊙O上![]() 的中点,证明∠1=∠2,再根据OA=OC,
的中点,证明∠1=∠2,再根据OA=OC,
得∠1=∠3,再得∠2=∠3,证明AD∥OC,最后得AD⊥CD,OC⊥CD,得到结论;
(2)设⊙O的半径为r,则OC=OB=r,再根据直角三角形边长关系求出r,最后用图中阴影部分的面积=S△COE﹣S扇形COB来计算.
(1)证明:连接OC,如图,
∵C为⊙O上![]() 的中点,
的中点,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠3,
∴∠2=∠3,
∴AD∥OC,
∴AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:设⊙O的半径为r,则OC=OB=r,
在Rt△OCE中,r2+(3![]() )2=(r+3)2,解得r=3,
)2=(r+3)2,解得r=3,
∴OC=3,OE=6,
∴∠E=30°,∠COE=60°,
∴图中阴影部分的面积=S△COE﹣S扇形COB
=![]() ×3×3
×3×3![]() ﹣
﹣![]()
=![]() .
.

练习册系列答案
相关题目
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答

①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.