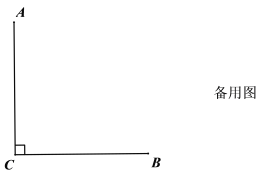��Ŀ����
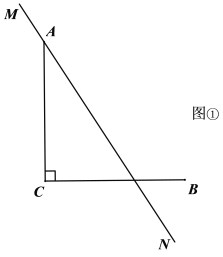
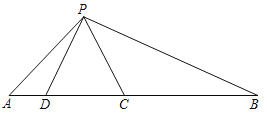
����Ŀ����֪��O�뾶Ϊ1������P�ڡ�O���ҡ�O�ϴ��ڵ�A��Bʹ�á�APB��60������Ƶ�P�ǡ�O������㣮
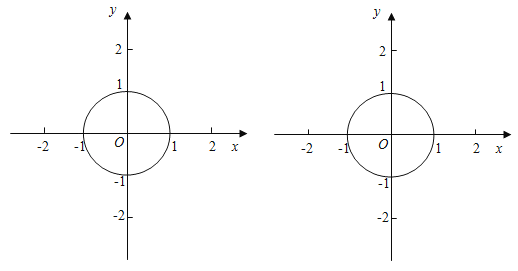
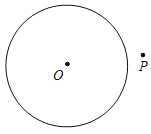
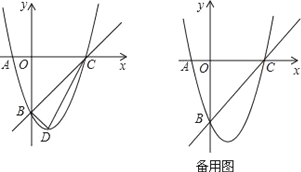
��1������������������ǰ�����������Ի�ͼ�����жϵ�P�Ƿ��ǡ�O������㣨�ں���������������������������
�ٵ�OP��1.2ʱ�� ��P�� ����O�������
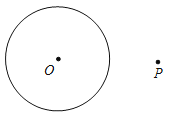
| �ڵ�OP��2ʱ�� ��P�� ����O�������
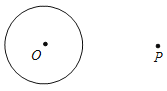
| �۵�OP��3ʱ�� ��P�� ����O�������
|
��2������P�ǡ�O������㣬��OP��ȡֵ��Χ���� ����
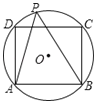
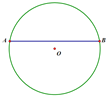
��3����ͼ����Բ��OΪ����ԭ�㽨��ƽ��ֱ������ϵxOy����ֱ��y����x+b��b��0����x�ᡢy��ֱ��ཻ�ڵ�M��N��
�����߶�MN������ֻ��һ�����ǡ�O������㣬��b��ֵ��
�����߶�MN�ϴ��ڡ�O������㣬��b��ȡֵ��Χ��
���𰸡���1�����ǣ����ǣ��۲��ǣ���2��1��OP��2����3����b��2![]() ����
����![]() ��b
��b![]()
��������
��1�����ݵ�P�ǡ�O�������Ķ��弴���жϣ�
��2����ͼ1�У������֪������P�պ��ǡ�O������㣬���P����O����������PA��PB֮��ļн�Ϊ60�������OP�ij����ɣ�
��3������ͼ2�У�����O��ֱ��y����x+b�ľ���OP��2ʱ���߶�MN������ֻ��һ�����ǡ�O������㣬���b��ֵ���ɣ�
�ڵ�ֱ�����O����ʱ�����е�ΪE�����b��ֵ�����жϣ�
�⣺��1���۲�ͼ�ο�֪ͼ�٢��У���P�ǡ�O������㣬ͼ���е�P���ǡ�O������㣮
�ʴ�Ϊ�ǣ��ǣ����ǣ�
��2�������֪������P�պ��ǡ�O������㣬���P����O����������PA��PB֮��ļн�Ϊ60������ͼ1��
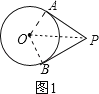
��PA��PB���O�ֱ������ڵ�A��B��
���OAP����OBP��90������APO����BPO��![]() ��APB��30����
��APB��30����
��OP��2OA��
���O�İ뾶Ϊr�����P�պ��ǡ�O�������ʱOP��2r��
��������P�ǡ�O������㣬���������1��OP��2��
��3������ͼ2�У�����O��ֱ��y����x+b�ľ���OP��2ʱ���߶�MN������ֻ��һ�����ǡ�O������㣬
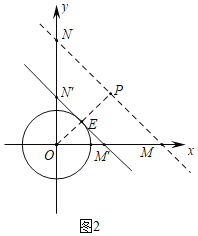
��M��b��0����N��0��b����
��OM��ON��
��OP��MN��
��PM��PN��
��OP��PM��PN��2��
��OM��ON��2![]() ��
��
��b��2![]() ��
��
�൱�߶�MN������ֻ��һ�����ǡ�O�������ʱ b��2![]() ��
��
�ڵ�ֱ�����O����ʱ�����е�ΪE��
��OE��EN����EM����1��
��ON����OM����![]() ��
��
�۲�ͼ���֪�����߶�MN�ϴ��ڡ�O������㣬b��ȡֵ��ΧΪ![]() ��b
��b![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�