题目内容
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且CD2=ADBC.
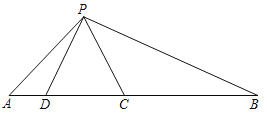
(1)求证:△APD∽△PBC;
(2)求∠APB的度数.
【答案】(1)见解析;(2)120°
【解析】
(1)CD2=ADBC可得AD:PC=PD:BC,又由△PCD是等边三角形,所以可求出∠ADP=∠BCP=120°,进而证明△ACP∽△PDB;
(2)由△APD∽△PBC,可得∠APD=∠B,则可求得∠APB的大小.
(1)证明:∵△PCD是等边三角形,
∴PD=PC=DC,∠PDC=∠PCD=60°,
∴∠ADP=∠BCP=120°,
∵CD2=ADBC,
∴AD:PC=PD:BC,
∴△APD∽△PBC;
(2)∵△APD∽△PBC,
∴∠APD=∠B,
∵∠B+∠BPC=60°,
∴∠APD+∠BPC=60°,
∴∠APB=60°+∠DPC=120°.

练习册系列答案
相关题目
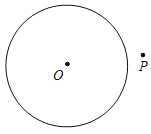
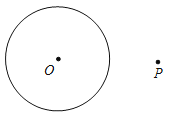
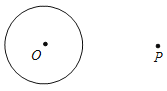
【题目】已知⊙O半径为1,若点P在⊙O外且⊙O上存在点A、B使得∠APB=60°,则称点P是⊙O的领域点.
(1)对以下情况,用三角板或量角器尝试画图,并判断点P是否是⊙O的领域点(在横线上填“是”或“不是”).
①当OP=1.2时, 点P ⊙O的领域点
| ②当OP=2时, 点P ⊙O的领域点
| ③当OP=3时, 点P ⊙O的领域点
|
(2)若点P是⊙O的领域点,则OP的取值范围是 ;
(3)如图,以圆心O为坐标原点建立平面直角坐标系xOy,设直线y=﹣x+b(b>0)与x轴、y轴分别相交于点M、N.
①若线段MN上有且只有一个点是⊙O的领域点,求b的值;
②若线段MN上存在⊙O的领域点,求b的取值范围.