题目内容
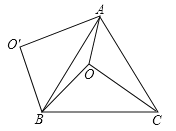
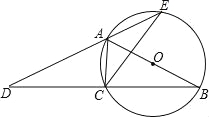
【题目】已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），如图所示．
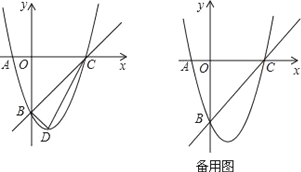
（1）求这个抛物线的解析式；
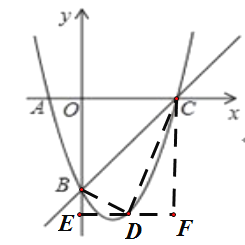
（2）若点D是直线BC下方抛物线上的动点，求△BCD面积最大时，点D的坐标及最大面积分别是多少？
【答案】（1）
；（2）D
,最大面积为
.
【解析】
（1）先解一元二次方程，然后用待定系数法求出抛物线解析式；
（2）先求出点C坐标，然后设D点为（x，y），过点D作DE⊥y轴，垂足为E，过点C作CF⊥DE，交DE于点F，利用间接法求△BCD的面积，得到面积与x的二次函数，然后利用二次函数的性质，化为顶点式，即可得到点D的坐标和面积的最大值.
解（1）∵x2+4x+3=0，
∴x1=-1，x2=-3，
∵m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，
∴m=-1，n=-3，
∵抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），
∴
，解得：
，
∴抛物线解析式为：；
（2）∵，
令
，则
，
解得：
或
，
∴点C坐标为：（3，0），
∵点B为（0，-3），
设D点坐标为：（x，y），点D在第四象限，
如图：过点D作DE⊥y轴，垂足为E，过点C作CF⊥DE，交DE于点F，
∴
，
，
，
，
，
∴
，
∴
整理，得：
，
∵
，且，
∴
，
∴
，
∴
；
∵
，
∴当
时，△BCD的面积取到最大值，
最大面积为：
；
∴
，
∴点D的坐标为：
；
∴点D的坐标为：；△BCD的最大面积为.
孟建平小学滚动测试系列答案
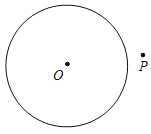
黄冈天天练口算题卡系列答案【题目】已知⊙O半径为1，若点P在⊙O外且⊙O上存在点A、B使得∠APB＝60°，则称点P是⊙O的领域点．
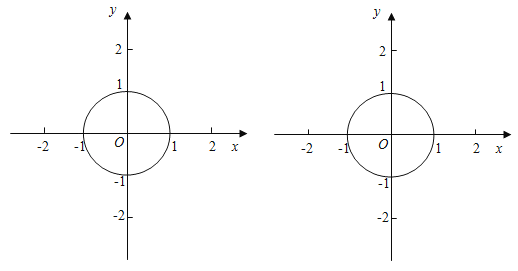
（1）对以下情况，用三角板或量角器尝试画图，并判断点P是否是⊙O的领域点（在横线上填“是”或“不是”）．
①当OP＝1.2时， 点P ⊙O的领域点
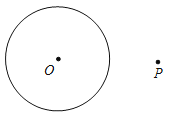
| ②当OP＝2时， 点P ⊙O的领域点
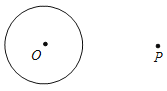
| ③当OP＝3时， 点P ⊙O的领域点
|
（2）若点P是⊙O的领域点，则OP的取值范围是 ；
（3）如图，以圆心O为坐标原点建立平面直角坐标系xOy，设直线y＝﹣x+b（b＞0）与x轴、y轴分别相交于点M、N．
①若线段MN上有且只有一个点是⊙O的领域点，求b的值；
②若线段MN上存在⊙O的领域点，求b的取值范围．
