Question

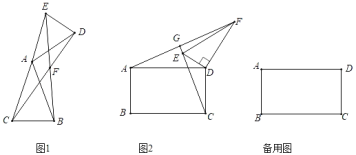
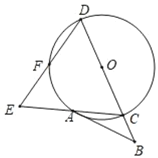
【题目】如图，AB与⊙O相切于点A，OB及其延长线交⊙O于C、D两点，F为劣弧AD上一点，且满足∠FDC=2∠CAB，延长DF交CA的延长线于点E．

(1)求证：DE=DC；

(2)若tan∠E=2，BC=1，求⊙O的半径．

Answer 1

【答案】(1)见解析；(2)⊙O的半径为

【解析】

（1）连接OA，AD，利用“三线合一”的逆定理即可证明DE=DC；

（2）易证△ACB∽△DAB，结合已知条件可得AB：BC=2，则可求出AB的长，设圆的半径为r，利用勾股定理可建立关于r的方程，解方程即可求出r的值．

解：(1)证明：连接OA，AD，

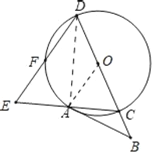
∵CD是为直径，

∴∠DAC=90°，

又∵AB为⊙O切线，

∴∠OAB=90°，

∴∠DAO=∠CAB，

∵∠EDC=2∠CAB，

∴∠EDC=2∠DAO，

∵DO=AO，

∴∠OAD=∠ODA，

∴∠EDC=2∠ADO，

∴AD平分∠EDC，

∵AD⊥EC，

∴DE=EC；

(2)∵∠CAB=∠ADB，∠B=∠B，

∴△ACB∽△DAB，

∴

又∵∠E=∠DCA，

∴tan∠DCA=2，

即

∴

∵BC=1，

∴AB=2，

设圆的半径为r，由勾股定理可得r2+22=(r+1)2，

解得：r=，

即⊙O的半径为．