题目内容
【题目】已知点E（x0，yo），点F（x2．y2），点M（x1，y1）是线段EF的中点，则x1＝
，y1＝
．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P1（即P，A，P1三点共线，且PA＝P1A），P1关于点B的对称点P2，P2关于点C的对称点P3，…按此规律继续以A，B，C三点为对称点重复前面的操作．依次得到点P4，P5，P6…，则点P2020的坐标是（ ）
A.（4，0）B.（﹣2，2）C.（2，﹣4）D.（﹣4，2）
【答案】B
【解析】
根据题意可得前6个点的坐标，即可发现规律每6个点一组为一个循环，根据2020÷6=336…4，进而可得点P2020的坐标．
解：∵A（1，﹣1），B（﹣1，﹣1），C（0，1），
点P（0，2）关于点A的对称点P1，
∴
，
，
解得x＝2，y＝﹣4，
所以点P1（2，﹣4）；
同理：
P1关于点B的对称点P2，
所以P2（﹣4，2）
P2关于点C的对称点P3，
所以P3（4，0），
P4（﹣2，﹣2），
P5（0，0），
P6（0，2），
…，
发现规律：
每6个点一组为一个循环，
∴2020÷6＝336…4，
所以点P2020的坐标是（﹣2，﹣2）．
故选：B．
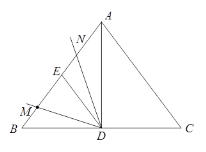
智趣寒假作业云南科技出版社系列答案
【题目】如图，在
中，
cm，
cm，点
为
的中点，点E为AB的中点．点
为AB边上一动点，从点B出发，运动到点A停止，将射线DM绕点顺时针旋转
度（其中
），得到射线DN，DN与边AB或AC交于点N．设
、两点间的距离为
cm，，
两点间的距离为
cm．
小涛根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．
下面是小涛的探究过程，请补充完整．
（1）列表：按照下表中自变量x的值进行取点、画图、测量，分别得到了与的几组对应值：
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
请你通过测量或计算，补全表格；
（2）描点、连线：在平面直角坐标系
中，描出补全后的表格中各组数值所对应的点
，并画出函数关于的图象．
（3）结合函数图象，解决问题：当
时，
的长度大约是 cm．（结果保留一位小数）
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？
