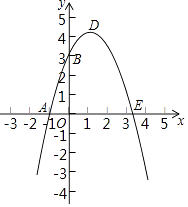题目内容
【题目】（1）有理数
在数轴上的位置如图所示，且
，化简：
．
（2）．已知在数轴上的位置如图所示，化简：
．
【答案】（1）b﹣a；（2）﹣a+c-b+1．
【解析】
（1）由数轴可知：b＞c＞0，a＜0，a+b=0，再根据有理数的运算法则，求出绝对值里的代数式的正负性，最后根据绝对值的性质化简．
（2）先根据数轴上各点的位置确定2a、a+c、1﹣b的符号，再根据绝对值的性质去掉绝对值符号，合并同类项即可．
（1）由数轴，得b＞c＞0，a＜0，又|a|=|b|，∴c﹣a＞0，c﹣b＜0，a+b=0．
|c﹣a|+|c﹣b|+|a+b|=c﹣a+b﹣c=b﹣a．
（2）∵a、c在原点的左侧，∴a＜0，c＜0，∴2a＜0，a+c＜0．
∵0＜b＜1，∴1﹣b＞0，∴原式=﹣2a+（a+c）+1﹣b=﹣2a+a+c+1﹣b=﹣a+c-b+1．
练习册系列答案
ABC考王全优卷系列答案
相关题目
