��Ŀ����
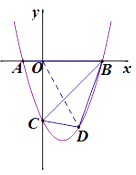
����Ŀ����ͼ��1����������y=ax2+bx+c��x�ύ��A��x1,0����B��x2,0�����㣨x1<0<x2������y�ύ�ڵ�C(0,-3),�������ߵĶԳ���Ϊֱ��x=1,��tan��OAC=3.
��1���������ߵĺ�������ʽ��
��2������D��������BC���ϵĶ��㣬�ҵ�D��ֱ��BC����Ϊ ![]() �����D������
�����D������
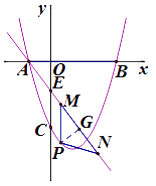
��3����ͼ��2������ֱ��y=mx+n������A,��y���ڵ�E(0, �� ![]() ),��P��ֱ��AE�·���������һ�㣬����P��x��Ĵ��߽�ֱ��AE�ڵ�M,��N���߶�AM�ӳ����ϣ���PM=PN,�Ƿ���ڵ�P��ʹ��PMN���ܳ������ֵ�������ڣ������P�����꼰��PMN���ܳ������ֵ����������,��˵������.
),��P��ֱ��AE�·���������һ�㣬����P��x��Ĵ��߽�ֱ��AE�ڵ�M,��N���߶�AM�ӳ����ϣ���PM=PN,�Ƿ���ڵ�P��ʹ��PMN���ܳ������ֵ�������ڣ������P�����꼰��PMN���ܳ������ֵ����������,��˵������.
���𰸡�
��1��
��Rt��AOC��tan ![]() OAC=
OAC= ![]() =3����OC=3��
=3����OC=3��
��OA=1��A��-1��0��
�������ߵĶԳ���Ϊֱ��x=1
�����е����깫ʽ���� ![]() �����x=3
�����x=3
��B��3��0��
����������ߵı���ʽΪ��y=a��x-3����x+1��
��C��0��-3��������ʽ�У�a����-3��=-3��
��ã�a=1
�������ߵı���ʽΪ��y=��x-3����x+1��=x2-2x-3
��2��
��B��3��0����C��0��-3��
�� ![]()
�� ![]()
��D��x��x2-2x-3��.����OD.
�� ![]()
= ![]()
= ![]()
= ![]()
=3
��ã�x1=1��x2=2
��D��1��-4����2��-3��
��3��
��A��-1,0����E��0��- ![]() ������
������
ֱ��AE�ı���ʽΪ��y= ![]() ��AE=
��AE= ![]()
��p��t��t2-2t-3������M��t�� ![]() t
t ![]() ��
��
��PM= ![]() t
t ![]() -��t2-2t-3��=- t2+
-��t2-2t-3��=- t2+ ![]()
��PG��MN��G��
��PM=PN�ã�MG=NG= ![]() MN
MN
�ɡ�PMG�ס�AEO�У� ![]() ����
���� ![]()
��MG= ![]() PM=NG
PM=NG
��C��PMN=PM+PN+MN= ![]() PM=
PM= ![]() ��- t2+
��- t2+ ![]() ��=-
��=- ![]() t2+
t2+ ![]() t+6
t+6
�൱t= ![]() ʱ��C��PMN�����ֵΪ
ʱ��C��PMN�����ֵΪ ![]() ����ʱP
����ʱP ![]()
����������1��C���������֪��tan��OAC���ݴ����A�����ꣻ�Գ�����x=1���ݴ����B�����ꡣ��2��B��C�������������֪����������֮��ľ��빫ʽ���BC�ij��ȣ���D��ֱ��BC�ľ���Ϊ ![]() ������
������ ![]() BCD��������D������ꡣ��3����֪A��E��������꣬���������ֱ��AE�ı���ʽ����֪P��M�ĺ�������ͬ���ֱ����P��M���㡣��PM�ֱ��ʾ��PN��MN�����ݶ��κ��������ʣ����
BCD��������D������ꡣ��3����֪A��E��������꣬���������ֱ��AE�ı���ʽ����֪P��M�ĺ�������ͬ���ֱ����P��M���㡣��PM�ֱ��ʾ��PN��MN�����ݶ��κ��������ʣ���� ![]() PMN�ܳ������ֵ����ʱP������ꡣ
PMN�ܳ������ֵ����ʱP������ꡣ
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

����Ŀ��ij�̳��O�ʽ�12.8��Ԫ��һ���Թ����յ����ʵ繲30̨�������г���Ҫ����Щ�յ����ʵ����ȫ�����ۣ�ȫ�����ۺ���������1.5��Ԫ�����пյ����ʵ�Ľ��ۺ��ۼۼ�����
�յ� | �ʵ� | |
���ۣ�Ԫ/̨�� | 5400 | 3500 |
�ۼۣ�Ԫ/̨�� | 6100 | 3900 |
���̳��ƻ������յ�x̨���յ��Ͳʵ�ȫ�����ۺ��̳���õ�����ΪyԪ��
��1����д��y��x�ĺ�����ϵʽ��
��2���̳����ļ��ֽ��������ɹ�ѡ��
��3��ѡ�����ֽ����������̳����������������Ƕ���Ԫ��



