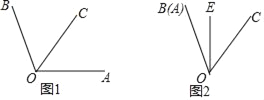题目内容
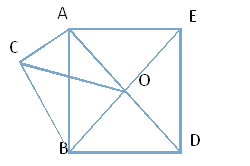
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系。
(1)请你写出上面问题中线段PG与PC的位置关系,并说明理由;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
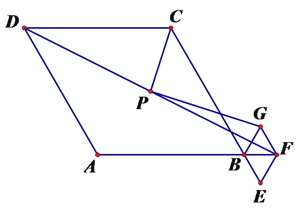
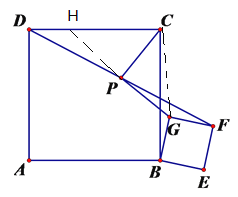
(3)将菱形ABCD和菱形BEFG均改成正方形,如图3,P为DF的中点,此时PG与PC的位置关系和数量关系分别是什么?直接写出答案。


【答案】(1)线段PG与PC的位置关系是PG⊥PC(2)没有发生变化 (3)PG⊥PC,PG=PC
【解析】分析:(1)根据题意可知小颖的思路为,通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件;
(2)思路同上,延长GP交AD于点H,连接CH,CG,本题中除了如(1)中证明△GFP≌△HDP(得到P是HG中点)外还需证明△HDC≌△GBC(得出三角形CHG是等腰三角形).
(3)思路同上,延长GP交CD于H,连接CG,证明△GFP≌△HDP即可.
详解:(1)线段PG与PC的位置关系是PG⊥PC.
理由:延长GP,交CD于点H,
∵四边形ABCD与四边形BEFG是菱形,
∴CD∥AB∥GF,
∴∠PDH=∠PFG,∠DHP=∠PGF,
∵P是线段DF的中点,
∴DP=PF,
在△DPH和△FGP中,
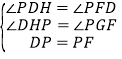 ,
,
∴△DPH≌△FGP(AAS),
∴PH=PG,DH=GF,
∵CD=BC,GF=GB=DH,
∴CH=CG,
∴CP⊥HG,
即PG⊥PC;

(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连接CH,CG,
∵P是线段DF的中点,
∴FP=DP,
∵AD∥FG,
∴∠GFP=∠HDP.
又∠GPF=∠HPD,
∴△GFP≌△HDP
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,∠HDC=∠ABC=60°.

由∠ABC=∠BEF=60°,且菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,
∴∠GBC=60°.
∴∠HDC=∠GBC.
∵四边形BEFG是菱形,
∴GF=GB.
∵△HDC≌△GBC.
∴CH=CG.
∴PH=PG,PG⊥PC.
(3)PG⊥PC,PG=PC.

【题目】某自行车厂一周计划生产1 400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.表是某周的生产情况(增产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +13 | ﹣10 | +16 | ﹣9 |
(1)根据记录的数据可知该厂星期五生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产了 辆自行车;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣15元,那么该厂工人这一周的工资总额是多少?