题目内容
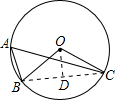
如图，⊙O是△ABC的外接圆，∠BAC=60°，若⊙O的半径0C为2，则弦BC的长为（ ）
| A．1 | B．
| C．2 | D．2
|
过O点作OD⊥BC，垂足为D，
∵∠BOC，∠BAC是
所对的圆心角和圆周角，
∴∠BOC=2∠BAC=120°，
∵OD⊥BC，
∴∠BOD=
∠BOC=60°，BC=2BD，
在Rt△BOD中，BD=OB•sin∠BOD=2×
=
，
∴BC=2BD=2
．
故选D．
∵∠BOC，∠BAC是
 |
| BC |
∴∠BOC=2∠BAC=120°，
∵OD⊥BC，
∴∠BOD=
| 1 |
| 2 |
在Rt△BOD中，BD=OB•sin∠BOD=2×
| ||
| 2 |
| 3 |
∴BC=2BD=2
| 3 |
故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
