题目内容
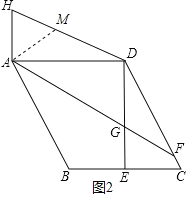
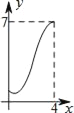
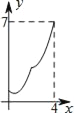
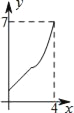
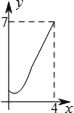
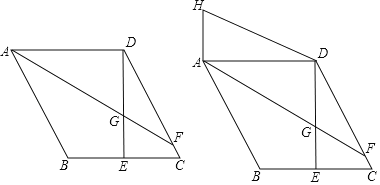
【题目】如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.
(1)若∠C=60°,AB=2,求GF的长;
(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.
【答案】(1)GF=1;(2)证明见解析.
【解析】
(1)过G作GH⊥CD于H,根据三角形的内角和得到∠CDE=60°,根据平行四边形的性质得到AD∥BC,AB=CD=2,得到∠ADC=120°,解直角三角形即可得到结论;
(2)根据全等三角形的性质得到∠ADH=∠EDC,∠H=∠C,DH=DC,根据平行四边形的性质得到AB=CD,AB∥CD,推出∠DFA=![]() ∠C,在DH上截取HM=AH,得到∠HAM=∠HMA,求得∠DAM=
∠C,在DH上截取HM=AH,得到∠HAM=∠HMA,求得∠DAM=![]() ∠H,根据全等三角形的性质即可得到结论.
∠H,根据全等三角形的性质即可得到结论.
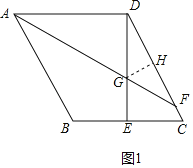
解:(1)如图1,过G作GH⊥CD于H,
∵DE⊥BC,
∴∠DEC=90°,
∵∠C=60°,
∴∠CDE=30°,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,
∴∠ADC=120°,
∵AD=DF,
∴∠DAF=∠DFA=30°,
∴∠GDF=∠DFG,
∴DG=GF,
∵CD=2,
∴DE=![]() CD=
CD=![]() ,
,
∴DF=![]() ,
,
∴HF=![]() DF=
DF=![]() ,
,
∴GF=1;
(2)∵AH⊥AD,DE⊥BC,
∴∠DAH=∠DEC=90°,
在△DAH与△DEC中,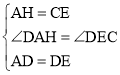 ,
,
∴△DAH≌△DEC(SAS),
∴∠ADH=∠EDC,∠H=∠C,DH=DC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DAB=∠C,∠DFA=∠BAF,
∵AD=DF,
∴∠DAF=∠DFA,
∴∠DFA=![]() ∠C,
∠C,
如图2,在DH上截取HM=AH,
∴∠HAM=∠HMA,
∴∠H=180°﹣2∠HAM,
∵∠MAD=90°﹣∠HAM,
∴∠DAM=![]() ∠H,
∠H,
∴∠MAD=∠GFD,
在△ADM与△FDG中,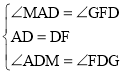 ,
,
∴△ADM≌△FDG(ASA),
∴DM=DG,
∵AB=CD=DH=HM+DM,
∴AB=AH+DG.