Question

【题目】已知ABCD，过点A作BC的垂线，垂足为E，∠BAE＝30°，BC＝2，AE＝，则点B到直线AC的距离为_____．

Answer 1

【答案】或1

【解析】

分两种情况, 进行讨论解答，第一种：作BF⊥AC于F，找到△ABC是等边三角形，再用勾股定理找到距离；第二种作BF⊥AC于F，BE＝1，AB＝2，∠ABE＝60°,得到BF＝BC＝1.

分两种情况：

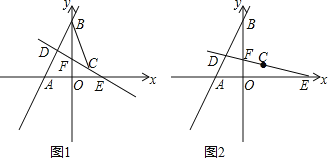
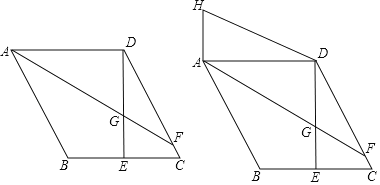
①如图1所示：作BF⊥AC于F，

∵AE⊥BC，

∴∠AEB＝90°，

∵∠BAE＝30°，AE＝，

∴BE＝1，AB＝2，∠ABE＝60°，

∵BC＝2＝AB，

∴△ABC是等边三角形，

∴AC＝BC＝2，

∵BF⊥AC，

∴CF＝AC＝1，

∴BF＝＝；

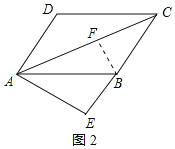
②如图2所示：作BF⊥AC于F，

∵AE⊥BC，

∴∠AEB＝90°，

∵∠BAE＝30°，AE＝，

∴BE＝1，AB＝2，∠ABE＝60°，

∵BC＝2＝AB，

∴∠BCA＝∠BAC＝30°，

∴BF＝BC＝1；

综上所述，点B到直线AC的距离为或1；

故答案为：或1．