题目内容
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )
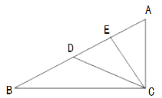
A. 5cm B. 6cm C. 7cm D. 8cm
【答案】A
【解析】
根据CE垂直平分AD,得AC=CD,再根据等腰三角形的三线合一,得∠ACE=∠ECD,结合角平分线定义和∠ACB=90°,得∠ACE=∠ECD=∠DCB=30°,则∠A=60°,进而求得∠B=30°,则BD=CD=AC.
因为CE垂直平分AD,
所以AC=CD=5cm.
所以∠ACE=∠ECD.
因为CD平分∠ECB,
所以∠ECD=∠DCB.
因为∠ACB=90°,
所以∠ACE=∠ECD=∠DCB=30°.
所以∠A=90°∠ACE=60°.
所以∠B=90°∠A=30°.
所以∠DCB=∠B.
所以BD=CD=5cm.
故选:A.

【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A | B | C | D | E | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.
【题目】为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
部分时段车流量情况调查表
时间 | 负责组别 | 车流总量 | 每分钟车流量 |
早晨上学6:30~7:00 | ①② | 2747 | 92 |
中午放学11:20~11:50 | ③④ | 1449 | 48 |
下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
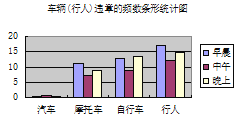
回答下列问题:
(1)请你写出2条交通法规.
(2)早晨.中午.晚上三个时段每分钟车流量的极差是多少,这三个时段的车流总量的中位数是多少.
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(4)通过分析写一条合理化建议.