题目内容
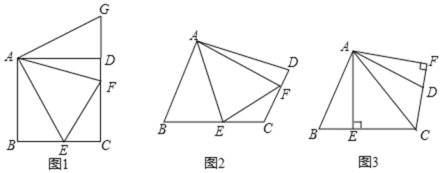
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).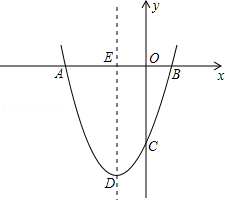
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),
将C点坐标(0,﹣3)代入,得:
a(0+3)(0﹣1)=﹣3,解得 a=1,
则y=(x+3)(x﹣1)=x2+2x﹣3,
所以抛物线的解析式为:y=x2+2x﹣3
(2)
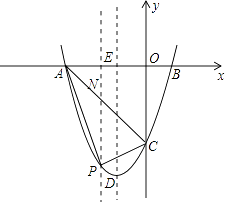
解:过点P作x轴的垂线,交AC于点N.
设直线AC的解析式为y=kx+m,由题意,得
![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为:y=﹣x﹣3.
设P点坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),
∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x.
∵S△PAC=S△PAN+S△PCN,
∴S= ![]() PNOA
PNOA
= ![]() ×3(﹣x2﹣3x)
×3(﹣x2﹣3x)
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,S有最大值
时,S有最大值 ![]() ,此时点P的坐标为(﹣
,此时点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y=x2+2x﹣3=y=(x+1)2﹣4,
∴顶点D的坐标为(﹣1,﹣4),
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(﹣4﹣0)2=20.
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图3①,
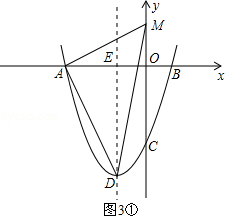
由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,
解得t= ![]() ,
,
所以点M的坐标为(0, ![]() );
);
②当D为直角顶点时,如图3②,
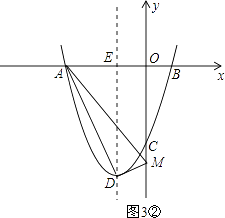
由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,
解得t=﹣ ![]() ,
,
所以点M的坐标为(0,﹣ ![]() );
);
③当M为直角顶点时,如图3③,
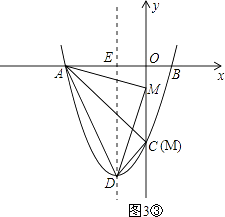
由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,
解得t=﹣1或﹣3,
所以点M的坐标为(0,﹣1)或(0,﹣3);
综可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0, ![]() )或(0,﹣
)或(0,﹣ ![]() )或(0,﹣1)或(0,﹣3)
)或(0,﹣1)或(0,﹣3)
【解析】(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x﹣3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?