Question

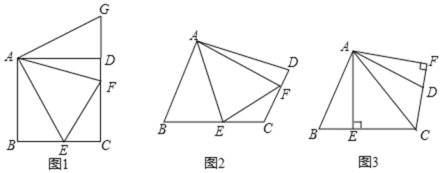
【题目】（1）如图 1，四边形 ABCD 中，∠BAD=∠ADC=∠CBA=90°，AB=AD，点 E、F 分别在四边形 ABCD 的边 BC、CD 上，∠EAF=45°，点 G 在 CD 的延长线上，BE=DG，连接 AG，求证：EF=BE+FD．

(2)如图 2，四边形 ABCD 中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点 E、F 分别在边BC、CD 上，则当∠BAD=2∠EAF 时，仍有 EF=BE+FD 成立吗？说明理由．

(3)如图 3，四边形 ABCD 中，∠BAD≠90°，AB=AD，AC 平分∠BCD，AE⊥BC 于 E，AF⊥CD 交 CD 延长线于 F，若 BC=9，CD=4，则 CE= ．（不需证明）

Answer 1

【答案】(1)见解析;(2)见解析;(3)见解析.

【解析】

（1）证明△ADG≌△ABE，根据全等三角形的性质得到AG=AE，∠DAG=

∠BAE，证明△AFG≌△AFE，得到GF=EF，证明结论；

（2）延长CB至 M，使 BM=DF，连接 AM，分别证明△ABM≌△ADF和△FAE≌△MAE，根据全等三角形的性质解答；

（3）证明 Rt△AEB≌Rt△AFD，根据全等三角形的性质得到BE=DF，根据题意列式计算．

（1）在△ADG和△ABE中，

，

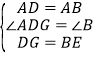∴△ADG≌△ABE（SAS），

∴AG=AE，∠DAG=∠BAE，

∵∠EAF=45°，即∠DAF+∠BEA=∠EAF=45°，

∴∠GAF=∠FAE，

在△GAF 和△FAE中，

，

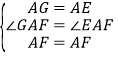∴△AFG≌△AFE（SAS），

∴GF=EF，

又∵DG=BE，

∴GF=BE+DF，

∴BE+DF=EF；

（2）EF=BE+DF．

理由如下：如图2所示，延长CB至M，使BM=DF，连接AM，

∵∠ABC+∠D=180°，∠ABC+∠ABM=180°，

∴∠D=∠ABM，

在△ABM和△ADF中，

，

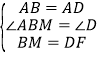∴△ABM≌△ADF（SAS），

∴AF=AM，∠DAF=∠BAM，

∵∠BAD=2∠EAF，

∴∠DAF+∠BAE=∠EAF，

∴∠EAB+∠BAM=∠EAM=∠EAF，

在△FAE和△MAE中，

，

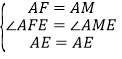∴△FAE≌△MAE（SAS），

∴EF=EM=BE+BM=BE+DF，即EF=BE+DF；

（3）∵AC平分∠BCD，AE⊥BC，AF⊥CD，

∴AE=AF，

在Rt△AEB和Rt△AFD中，

，

∴Rt△AEB≌Rt△AFD（HL），

∴BE=DF，

由题意得，CE+BE=9，CE﹣BE=4，

解得，CE=6.5，

故答案为：6.5．