题目内容
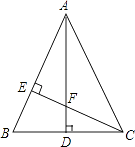
【题目】如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.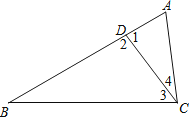
【答案】解:∵△ADC与△DBC同高,且△ADC与△DBC的面积比为1:3,AD=3,
∴BD=9,
∴AB=12,
∵AC=6,
∴ ![]()
∵∠A=∠A,
∴△ADC∽△ACB,
∴∠ACD=∠B.
【解析】由于△ADC与△DBC同高,且△ADC与△DBC的面积比为1:3,AD=3,可求出BD=9,推得AB=12,有相似三角形的判定证得△ADC∽△ACB,再由相似三角形的判定可推得结论.本题主要考查了三角形的面积,相似三角形的判定和性质,灵活应用相似三角形的判定和性质是解决问题的关键.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
相关题目
【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
成绩(分) | 46 | 47 | 48 | 49 | 50 |
人数(人) | 1 | 2 | 1 | 2 | 4 |
下列说法正确的是( )
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48