题目内容
【题目】如图，抛物线y=﹣x2+bx+c与x轴相交于A，B两点，与y轴相交于点C（0，3），点B坐标是（3，0），设抛物线的顶点为点D．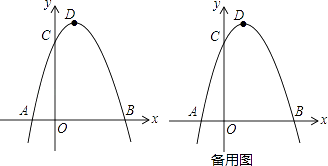
（1）求此抛物线的解析式与对称轴；
（2）作直线BC，与抛物线的对称轴交于点E，点P为直线BC上方的二次函数上一个动点（且点P与点B，C不重合），过点P作PF∥DE交直线BC于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PDEF为平行四边形？
②设△PBC的面积为S，求S与m的函数关系式．S是否存在最大值？若存在，求出最大值并求出此时P点坐标，若不存在，说明理由．
【答案】
（1）
解：将点C（0，3）、B（3，0）代入抛物线的解析式得： 
，
解得： 
，
抛物线的解析式为y=﹣x2+2x+3．
∵x=﹣ 
，
∴x=﹣ 
=1．
∴抛物线的对称轴为x=1
（2）
解：①如图1所示：
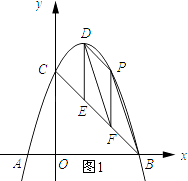
∵将x=1代入得抛物线的解析式得y=4．
∴点D的坐标为（1，4）．
设直线BC的解析式为ykx+b，将点B、C的坐标代入得： 
，
解得： 
．
∴直线BC的解析式为y=﹣x+3．
将x=1代入y=﹣x+3得：y=﹣1+3=2．
∴点E的坐标为（1，2）．
∴DE=2．
∵点P的横坐标为m，
∴yp=﹣m2+2m+3，yF=﹣m+3．
∴PF=yp﹣yF=﹣m2+3m．
∵四边形PDEF为平行四边形，
∴PF=DE=2，即﹣m2+3m=2．
解得：m=2或m=1（舍去）．
∴当m=2时，四边形PDEF为平行四边形．
②存在：
理由：如图2所示：
= 
=﹣ 
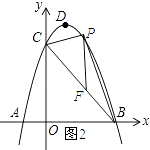
（m2﹣3m）=﹣ 
+ 
．
当m= 时，△PBC的面积由最大值，最大值为 ．
∵将x= 代入抛物线的解析式得：y= 
．
∴点P的坐标为（ ， ）
【解析】（1）将点C（0，3）、B（3，0）代入抛物线的解析式可求得得： ，从而求得抛物线的解析式为y=﹣x2+2x+3，由x=﹣ 可求得抛物线的对称轴方程为x=1；（2）①如图1所示：先求得点D的坐标，然后依据待定系数法求得直线BC的解析式为y=﹣x+3，将x=1代入y=﹣x+3得y=2，从而得到ED=2，由点P的横坐标为m，可求得yp=﹣m2+2m+3，yF=﹣m+3．故此PF=yp﹣yF=﹣m2+3m．当PF=DE=2时四边形PDEF为平行四边形，从而可求得m=2；
②由 可知S=﹣ + ，故此可知当m= 时，最大值为 ．将x= 代入抛物线的解析式得：y= ．故此可知点P的坐标为（ ， ）．
【考点精析】关于本题考查的函数关系式和二次函数的图象，需要了解用来表示函数关系的数学式子叫做函数解析式或函数关系式；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案．
