题目内容
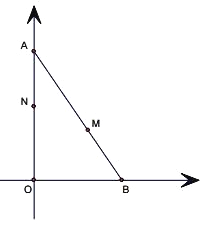
【题目】如图,己知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
(1)当t为何值时,M为AB的中点;
(2)当t为何值时,△AMN为直角三角形;
(3)当t为何值时,△AMN是等腰三角形?并求此时点M的坐标.
【答案】(1)当t=![]() 秒时,M是AB的中点;(2)当
秒时,M是AB的中点;(2)当![]() 或
或![]() 时,△AMN为直角三角形;
时,△AMN为直角三角形;
(3)当![]() ,
,![]() ,
, ![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由勾股定理求出AB的长,再由中点的定义即可得出结论;
(2)运动t秒时,AN=t,BM=2t,AM=10-2t.然后分两种情况讨论:①当MN⊥AO时,△ANM∽△AOB;②当MN⊥AB时,△ANM∽△ABO;
(3)先求出M的坐标,然后分三种情况讨论:①AM=AN;②MA=MN;③NA=NM.
(1)∵A(0,8),B(6,0),∴OA=8,OB=6,∴AB=10.
∵M为AB的中点,∴MB=2t=5,∴t=![]() .
.
答:当t=![]() 秒时,M是AB的中点.
秒时,M是AB的中点.
(2)运动t秒时,AN=t,BM=2t,AM=10-2t.
①当MN⊥AO时,△ANM∽△AOB,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
②当MN⊥AB时,△ANM∽△ABO,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
综上:当 t=![]() 或 t=
或 t=![]() 时,△AMN为直角三角形.
时,△AMN为直角三角形.
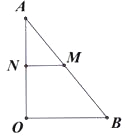
(3)如图,过M作MC⊥OB于C,MD⊥OA于D.
∵AO⊥OB,∴∠MCB=∠AOB.
∵∠MBC=∠ABO,∴△MBC∽△ABO,∴![]() ,∴
,∴![]() ,∴MC=
,∴MC=![]() ,CB=
,CB=![]() ,∴OC=
,∴OC=![]() ,∴M(
,∴M(![]() ,
,![]() ).分三种情况讨论:
).分三种情况讨论:
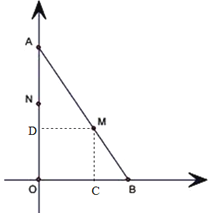
①当AM=AN时,t=102t,解得:![]() ,∴M(2,
,∴M(2,![]() );
);

②当MA=MN时,过M作MF⊥AO,交AO于F,如图:
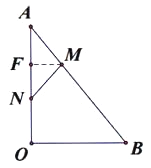
则F是AN的中点,AF=![]() ,这时,△AFM∽△AOB,∴
,这时,△AFM∽△AOB,∴![]() ,∴
,∴![]() ,解得
,解得 ![]() ,∴M(
,∴M(![]() ,
,![]() );
);
③当NA=NM时,过N作NG⊥AB,交AB于G,如图,则G是AM的中点,AG=5t.
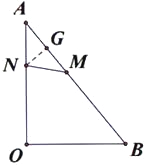
这时,△AGN∽△AOB,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴M(
,∴M(![]() ,
,![]() ).
).
综上,当 ![]() 或
或![]() 或
或![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() .
.