��Ŀ����
����Ŀ�� ��������ABCD�У�
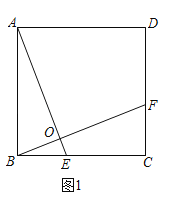
��1����ͼ1����E��F�ֱ���BC��CD�ϣ�AE��BF�ཻ�ڵ�O����AOB=90�㣬���ж�AE��BF��������ϵ����˵�����ɣ�
��2����ͼ2����E��F��G��H�ֱ��ڱ�BC��CD��DA��AB�ϣ�EG��FH�ཻ�ڵ�O����GOH=90�㣬��EG=7����FH�ij���
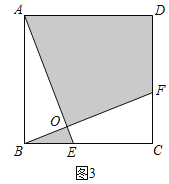
��3����ͼ3����E��F�ֱ���BC��CD�ϣ�AE��BF�ཻ�ڵ�O����AOB=90�㣬��AB=5��ͼ����Ӱ���ֵ�����������ε����֮��Ϊ4��5�����ABO���ܳ���

���𰸡���1��AE=BF�����ɼ���������2��FH=7����3����AOB���ܳ�Ϊ5+![]()
��������
��1�����ı���ABCD�������οɵ�AB=BC����ABE=��BCF=90����������ǵ����ʿɵá�BAO=��CBF��Ȼ�����ASA��֤��ABE�ա�BCF�������ɵý��ۣ�
��2����ͼ4���������ߣ�����ƽ���ı���AMEG��ƽ���ı���BNFH����AM=GE��BN=FH���ɣ�1����Ľ���֪��ABM�ա�BCN�������ɵ�FH�ij���
��3�����������ε��������Ӱ���ֵ�����ɵã��հײ��ֵ����Ϊ25��20=5���á�AOB��������ı���OECF�������ȣ���AO=a��BO=b������ab=5�����ݹ��ɶ����ã�a2+b2=52��Ȼ�������ȫƽ����ʽ�������a+b����һ�����ý����
�⣺��1��AE=BF�������ǣ���ͼ1�����ı���ABCD�������Σ�
��AB=BC����ABE=��BCF=90����
�ߡ�AOB=90�������BAO+��ABO=90����
�֡ߡ�CBF+��ABO=90�������BAO=��CBF��
���ABE�ա�BCF��ASA����
��AE=BF��
��2����ͼ2�У�����A��AM��GE��BC��M������B��BN��FH��CD��N��AM��BN���ڵ�O������ͼ4�����ı���AMEG���ı���BNFH��Ϊƽ���ı��Σ�
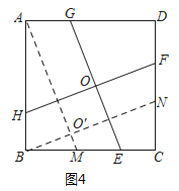
��AM=GE��BN=FH��
�ߡ�GOH=90����AM��GE��BN��FH�����AO��B=90����
�ɣ�1���ã���ABM�ա�BCN����AM=BN��
��FH=GE=7��
��3����ͼ3������Ӱ���ֵ������������ABCD�����֮��Ϊ4��5��
����Ӱ���ֵ����Ϊ![]() ��25=20����հײ��ֵ����Ϊ25��20=5��
��25=20����հײ��ֵ����Ϊ25��20=5��
�ɣ�1���ã���ABE�ա�BCF��
���AOB��������ı���OECF�������ȣ���Ϊ![]() ��5=
��5=![]() ��
��
��AO=a��BO=b����![]() ab=
ab=![]() ����ab=5��
����ab=5��
��Rt��AOB����AOB=90������a2+b2=52��
��a2+2ab+b2=25+10=35����![]() ��
��
��a+b=![]() ����AO+BO=
����AO+BO=![]() ��
��
���AOB���ܳ�Ϊ5+![]() ��
��

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�����Ŀ�����о��С���ʮ�߽���Сѧ���鷨��������Ʒ��������֪ÿ��������Ʒ�ɼ���Ϊ![]() ����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ��.
����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ��.
������ | Ƶ�� | �ٷֱ� |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
�ϼ� | 100 | 1 |
�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ

����������Ϣ������������⣺
(1)����ѱ��пհ״���������д����.
(2)�벹ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ.
(3)��80��(��80��)���ϵ��鷨��Ʒ������Ϊ�ȼ������Թ���ȫ�л�õȼ��ķ���.