题目内容
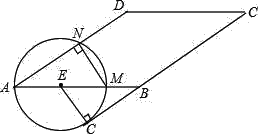
【题目】如图,平面直角坐标系中,以点M(4,0)为圆心,MO为半径的半圆交x轴于点A,P为半圆上的一个动点,以点P为直角顶点在OP上方作Rt△OPB,且OP=2PB,OB交半圆于点Q.

(1)当P为半圆弧的中点时,求△OPB的面积.
(2)在运动过程中,求MB的最大值.
(3)在运动过程中,若点Q将线段OB分为1:2的两部分,求出此时点P的坐标.
【答案】(1)8;(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由P为半圆弧的中点可知PM⊥OA,P(4,4),根据勾股定理求得OP=4![]() , 由已知条件可得PB=2
, 由已知条件可得PB=2![]() , 根据三角形的面积公式计算即可.
, 根据三角形的面积公式计算即可.
(2)连结AP,易证得B,P,A三点共线;在△OAB中,两高线OP和AQ的交点C,则BC垂直于x轴,易得BM≤BC+CM,当B,C,M在同一直线上时,BM=BC+CM,BM取得最大值,求出此时的BM值即可.
(3)由点Q将线段OB分为1:2的两部分,可知OQ:BQ=2:1或OQ:BQ=1:2;连接AQ,设出未出知数,结合△OPB~△AQB,用未知数表示出AP和OP;在Rt△OAP中,由勾股定理构造方程解出未知数;并相应的求出点P的横、纵坐标即可.
(1)∵P为半圆弧的中点,M(4,0),⊙M半径为4,
∴P(4,4),PM⊥OA,
∴OP=![]() ,
,
∵OP=2PB,
∴PB=2![]() ,
,
在Rt△OPB中,
∴SRt△OPB=![]() ×PB×OP=
×PB×OP=![]() .
.
∴△OPB的面积为8.
(2)连结AP,AQ交OP于点C,
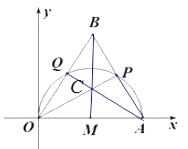
∵OA是半圆M的直径,
∴∠APO=∠AQO=90°,
又∵∠OPB=90°,
∴∠OPB+∠APO=180°,
∴点B,P,A三点共线,
连结BC,CM,BM,
∵在△OAB中,AQ和OP都是△OAB的高线,C是AQ和OP的交点,
∴直线BC⊥OA,
∵BM≤BC+CM,
∴当B,C,M在同一直线上时,BM=BC+CM,BM取得最大值,此时BM⊥OA,
又∵OM=AM,
∴OB=AB.
设BP=x,则OP=2x,AB=OB=![]() x,AP=
x,AP=![]() x-x=(
x-x=(![]() -1)x,
-1)x,
在Rt△OPA中,∵OP2+AP2=OA2 ,
∴(2x)2+(![]() -1)x2=82 ,
-1)x2=82 ,
解得x2=![]() .
.
在Rt△OBM中,
∵BM2=OB2-OM2 ,
∴BM=![]()
(3)连结AQ,过点P作PN⊥OA于N,

①当OQ:BQ=2:1,设BP=3x,则OP=6x,OB=![]() x,则OQ=2
x,则OQ=2![]() x,BQ=
x,BQ=![]() x.
x.
∵∠OPB=∠AQB=90°,∠B=∠B,
∴△OPB~△AQB,
∴![]() ,
,
则![]() ,即AB=5x,
,即AB=5x,
则AP=AB-BP=2x,
在Rt△OPA中,由OP2+AP2=OA2 , 得(6x)2+(2x)2=82 ,
解得x2=![]()
∵S△OPA=![]() ,
,
∴PN=![]() ,
,
则ON=![]() ,
,
∴点P(![]() ,
,![]() ).
).
②当OQ:BQ=1:2,设BP=3x,则OP=6x,OB=3![]() x,则OQ=
x,则OQ=![]() x,BQ=2
x,BQ=2![]() x.
x.
∵∠OPB=∠AQB=90°,∠B=∠B,
∴△OPB~△AQB,
∴![]() ,
,
则![]() ,即AB=10x,
,即AB=10x,
则AP=AB-BP=7x,
在Rt△OPA中,由OP2+AP2=OA2 , 得(6x)2+(7x)2=82 ,
解得x2=![]() .
.
∵S△OPA=![]() ,
,
∴PN=![]() ,
,
则ON=![]() ,
,
∴点P(![]() ,
,![]() ).
).
综上所述,P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案