Question

【题目】如图1，在中，，，，于，点是线段上一动点，点与点在直线两侧，，，点在边上，，连接，，．

（1）依题意，补全图形；

（2）求证：；

（3）请在图2中画出图形，确定点的位置，使得有最小值，并直接写出的最小值为________．

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析，的最小值为10．

【解析】

（1）根据题目要求作图即可；

（2）根据等腰三角形的性质和垂直的定义求出∠MAD＝∠C，利用SAS证明△AMD≌△CEB即可得出结论；

（3）根据，判断出当B、M、D三点共线时，的值最小，BD的长即为的最小值，作出图形，然后根据勾股定理求出BD即可．

解：（1）补全图形，如图1所示：

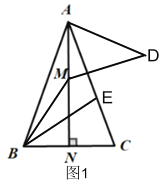
（2）∵AD⊥AB，

∴∠MAD＋∠BAN＝90°，

∵AB＝AC，AN⊥BC，

∴∠BAN＝∠CAN，∠CAN＋∠C＝90°，

∴∠MAD＝∠C，

又∵AD＝BC，AM＝CE，

∴△AMD≌△CEB（SAS），

∴；

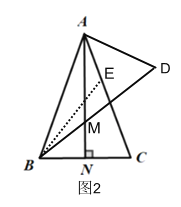
（3）点M位置如图2所示；

由（2）可知：△AMD≌△CEB，

∴MD＝BE，AD＝BC＝6，

∴，

∵，

∴当B、M、D三点共线时，的值最小，BD的长即为的最小值，

∵∠BAD＝90°，

∴，

即的最小值为10．