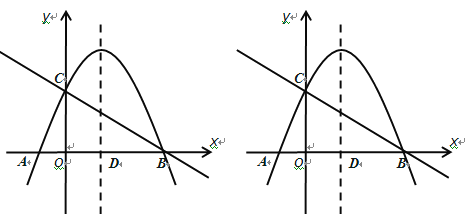题目内容
【题目】如图，二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点，与y轴交于C点，且对称轴为直线x=1，点B坐标为(－1，0)．则下面的四个结论：①2a+b=0；②4a－2b+c＜0；③ac＞0；④当y＜0时，x＜－1或x＞3．其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】∵抛物线的对称轴是x=1，∴
，∴2a+b=0，故①正确；
∵抛物线开口向下，∴a＜0，
∵B（-1，0），∴当x=-2时，y<0，即4a-2b+c<0，故②正确；
∵抛物线与y轴的交点在x轴上方，∴c＞0， ∴ac＜0，故③错误；
∵对称轴为直线x=1，点B坐标为(－1，0)，∴点A（3，0），∴当y＜0时，x＜－1或x＞3，故④正确，
所以正确的有3个，
故选C.
练习册系列答案
相关题目
【题目】某公司为一种新型电子产品在该城市的特约经销商，已知每件产品的进价为40元，该公司每年销售这种产品的其他开支（不含进货价）总计100万元，在销售过程中得知，年销售量y（万件）与销售单价x（元）之间存在如表所示的函数关系，并且发现y是x的一次函数．
销售单价x（元） | 50 | 60 | 70 | 80 |
销售数量y（万件） | 5.5 | 5 | 4.5 | 4 |
（1）求y与x的函数关系式；
（2）问：当销售单价x为何值时，该公司年利润最大？并求出这个最大值；
【备注：年利润=年销售额﹣总进货价﹣其他开支】
（3）若公司希望年利润不低于60万元，请你帮助该公司确定销售单价的范围．