题目内容
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

【答案】(1)见解析;(2)MB=MC.理由见解析;(3)MB=MC还成立,见解析.
【解析】
(1)连接AM,根据全等三角形的对应边相等可得AD=AE,AB=AC,全等三角形对应角相等可得∠BAD=∠CAE,再根据等腰三角形三线合一的性质得到∠MAD=∠MAE,然后利用“边角边”证明△ABM和△ACM全等,根据全等三角形对应边相等即可得证;
(2)延长DB、AE相交于E′,延长EC交AD于F,根据等腰三角形三线合一的性质得到BD=BE′,然后求出MB∥AE′,再根据两直线平行,内错角相等求出∠MBC=∠CAE,同理求出MC∥AD,根据两直线平行,同位角相等求出∠BCM=∠BAD,然后求出∠MBC=∠BCM,再根据等角对等边即可得证;
(3)延长BM交CE于F,根据两直线平行,内错角相等可得∠MDB=∠MEF,∠MBD=∠MFE,然后利用“角角边”证明△MDB和△MEF全等,根据全等三角形对应边相等可得MB=MF,然后根据直角三角形斜边上的中线等于斜边的一半证明即可.
(1)如图(2),连接AM,由已知得△ABD≌△ACE,
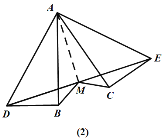
∴AD=AE,AB=AC,∠BAD=∠CAE.
∵MD=ME,
∴∠MAD=∠MAE,
∴∠MAD-∠BAD=∠MAE-∠CAE,
即∠BAM=∠CAM.
在△ABM和△ACM中,
AB=AC,
∠BAM=∠CAM,
AM=AM,
∴△ABM≌△ACM(SAS),
∴MB=MC.
(2)MB=MC.
理由如下:如图(3),延长CM交DB于F,延长BM到G,使得MG=BM,连接CG.
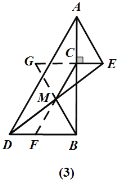
∵CE∥BD,
∴∠MEC=∠MDF,∠MCE=∠MFD.
∵M是ED的中点,
∴MD=ME.
在△MCE和△MFD中,
∠MCE=∠MFD,
∠MEC=∠MDF,
MD=ME,
∴△MCE≌△MFD(AAS).
∴MF=MC.
∴在△MFB和△MCG中,
MF=MC,
∠FMB=∠CMG,
BM=MG,
∴△MFB≌△MCG(SAS).
∴FB=GC,∠MFB=∠MCG,
∴CG∥BD,即G、C、E在同一条直线上.
∴∠GCB=90°.
在△FBC和△GCB中,
FB=GC,
∠FBC=∠GCB,
BC=CB,
∴△FBC≌△GCB(SAS).
∴FC=GB.
∴MB=![]() GB=
GB=![]() FC=MC.
FC=MC.
(3)MB=MC还成立.
如图(4),延长BM交CE于F,延长CM到G,使得MG=CM,连接BG.
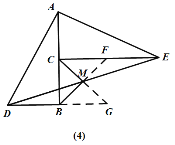
∵CE∥BD,
∴∠MDB=∠MEF,∠MBD=∠MFE.
又∵M是DE的中点,
∴MD=ME.
在△MDB和△MEF中,
∠MDB=∠MEF,
∠MBD=∠MFE,
MD=ME,
∴△MDB≌△MEF(AAS),
∴MB=MF.
∵CE∥BD,
∴∠FCM=∠BGM.
在△FCM和△BGM中,
CM=MG,
∠CMF=∠GMB,
MF=MB,
∴△FCM≌△BGM(SAS).
∴CF=BG,∠FCM=∠BGM.
∴CF//BG,即D、B、G在同一条直线上.
在△CFB和△BGC中,
CF=BG,
∠FCB=∠GBC,
CB=BC,
∴△CFB≌△BGC(SAS).
∴BF=CG.
∴MC=![]() CG=
CG=![]() BF=MB.
BF=MB.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案【题目】由于雾霾天气持续笼罩某地区,口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩,销售完后共获利2800元,其进价和售价如下表:
甲种口罩 | 乙种口罩 | |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该商店购进甲、乙两种口罩各多少袋?
(2)该商店第二次仍以原价购进甲、乙两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍,甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,则乙种口罩最低售价为每袋多少元?