题目内容
【题目】如图1,将![]() 纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
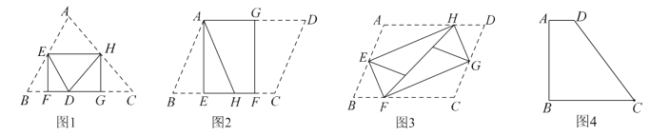
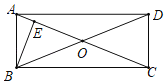
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_______,__________;
,则操作形成的折痕分别是线段_______,__________;![]() ___________.
___________.
(2)将![]() 纸片按图3的方式折叠成一个叠合矩形
纸片按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
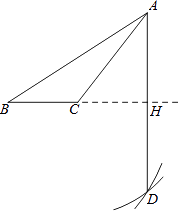
(3)如图4,四边形![]() 纸片满足
纸片满足![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出
,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出![]() 、
、![]() 的长.
的长.
【答案】(1)AE,GF,1:2;(2)13;(3)AD =1,BC =7;
【解析】
(1)根据题意得出操作形成的折痕分别是线段AE、GF;由折叠的性质得出△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,得出S矩形AEFG=![]() SABCD,即可得出答案;
SABCD,即可得出答案;
(2)由矩形的性质和勾股定理求出FH,即可得出答案;
(3)由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,由叠合正方形的性质得出BM=FM=4,由勾股定理得出GM=CM=
CD=5,GM=CM,∠FMC=90°,由叠合正方形的性质得出BM=FM=4,由勾股定理得出GM=CM=![]() =3,得出AD=BG=BM-GM=1,BC=BM+CM=7;
=3,得出AD=BG=BM-GM=1,BC=BM+CM=7;
解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
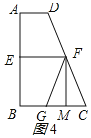
∴S矩形AEFG=![]() SABCD,
SABCD,
∴S矩形AEFG:SABCD=1:2;
故答案为:AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH=![]() =13,
=13,
由折叠的性质得:AD=FH=13;
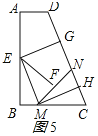
(3)图5所示:
如图4所示:由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,
CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
∴BM=FM=4,
∴GM=CM=![]() =3,
=3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案