题目内容
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
【答案】
(1)解:所求作△A1B1C如图所示:
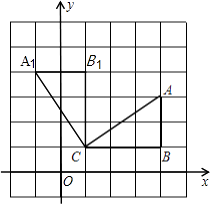
由A(4,3)、B(4,1)可建立如图所示坐标系,
则点A1的坐标为(﹣1,4),点B1的坐标为(1,4)
(2)解:∵AC= ![]() =
= ![]() =
= ![]() ,∠ACA1=90°
,∠ACA1=90°
∴在旋转过程中,△ABC所扫过的面积为:
S扇形CAA1+S△ABC
= ![]() +
+ ![]() ×3×2
×3×2
= ![]() +3.
+3.
【解析】(1)根据旋转中心旋转方向及旋转角度找出点A、B的对称点A1、B1的位置,然后顺次连接即可,根据A、B的坐标建立坐标系,据此写出点A1、B1的坐标;(2)用勾股定理得出AC的长度,在旋转过程中,△ABC所扫过的面积为:S扇形CAA1+S△ABC计算即可。
【考点精析】认真审题,首先需要了解扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.