题目内容
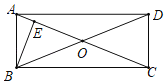
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等角对等边得出OB=OC,根据平行四边形性质求出OC=OA=![]() AC,OB=OD=
AC,OB=OD=![]() BD,推出AC=BD,根据矩形的判定推出即可.
BD,推出AC=BD,根据矩形的判定推出即可.
(2)根据矩形的性质和∠CBE=3∠ABE,得出∠ABE=22.5°,在EB上取一点H,使得EH=AE,易证AH=BH,设AE=EB=x,则AH=BH=![]() x,构建方程即可解决问题.
x,构建方程即可解决问题.
(1)证明:∵∠OBC=∠OCB,
∴OB=OC,
∵四边形ABCD是平行四边形,
∴OC=OA=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴AC=BD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠CBE=3∠ABE,
∴∠ABE=![]() ×90°=22.5°,
×90°=22.5°,
∵BE⊥AO,
∠BAE=90°-∠ABE=67.5°,
在EB上取一点H,使得EH=AE,
∴∠HAE=∠AHE=45°,
∴∠BAH=∠BAE-∠HAE=22.5°,
∴∠BAH=∠ABE=22.5°,
∴AH=BH,
设AE=EB=x,则AH=BH=![]() =
=![]() x,
x,

∵BE=2,
∴x+![]() x=2,
x=2,
∴x=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目