题目内容
【题目】有6张看上去无差别的卡片,上面分别写着1、2、3、4、5、6
(1)一次性随机抽取2张卡片,用列表或画树状图的方法求出“两张卡片上的数都是偶数”的概率
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,直接写出“第二次取出的数字小于第一次取出的数字”的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)用列表法举出所有情况,看两张卡片上的数都是偶数的情况占总情况的多少即可;
(2)画出树形图即可求出第二次取出的数字小于第一次取出的数字的概率.
解:(1)依题意列表如下:
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 2,1 | 3,1 | 4,1 | 5,1 | 6,1 | |
2 | 1,2 | 3,2 | 4,2 | 5,2 | 6,2 | |
3 | 1,3 | 2,3 | 4,3 | 5,3 | 6,3 | |
4 | 1,4 | 2,4 | 3,4 | 5,4 | 6,4 | |
5 | 1,5 | 2,5 | 3,5 | 4,5 | 6,5 | |
6 | 1,6 | 2,6 | 3,6 | 4,6 | 5,6 |
由上表可知,随机抽取2张卡片可能出现的结果有15个,它们出现的可能性相等,其中“两张卡片上的数都是偶数”的结果有3个,
所以P(两张卡片上的数都是偶数)=![]() ;
;
(2)画树形图得:
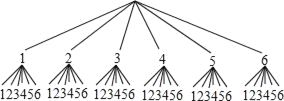
随机抽取2张卡片可能出现的结果有36个,第二次取出的数字小于第一次取出的数字有15种,所以其概率=![]() .
.

【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
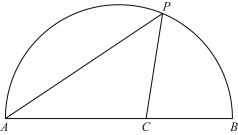
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).