Question

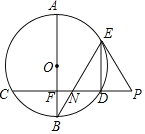
【题目】在⊙O中，直径AB⊥弦CD于点F，点E是弧AD上一点，连BE交CD于点N，点P在CD的延长线上，PN＝PE．

（1）求证：PE是⊙O的切线；

（2）连接DE，若DE∥AB，OF＝3，BF＝2，求PN的长．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）连接OE，由等腰三角形的性质得出∠PEN＝∠PNE＝∠BNF，∠OEB＝∠OBE．证出∠OEB+∠PEN＝90°，即PE⊥OE，即可得出结论；

（2）连接CE，证出CE为⊙O的直径．由垂径定理得出CF＝DF，得出DE＝2OF＝6．求出OC＝OB＝5，CE＝10，由勾股定理得出CD＝8．设PD＝x，则PC＝x+8．在Rt△PDE和Rt△PCE中，由勾股定理得出方程，解方程求出PD＝，由勾股定理即可得出答案．

（1）证明：连接OE，如图1所示：

∵PN＝PE，

∴∠PEN＝∠PNE＝∠BNF，

∵OE＝OB，

∴∠OEB＝∠OBE．

∵AB⊥CD，

∴∠OBE+∠BNF＝90°，

∴∠OEB+∠PEN＝90°，

即∠OEP＝90°，

∴PE⊥OE，

∴PE是⊙O的切线．

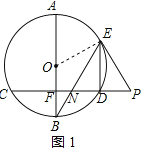
（2）解：连接CE，如图2所示：

∵DE∥AB，AB⊥CD，

∴∠EDC＝90°

∴CE为⊙O的直径．

∵AB⊥CD，

∴CF＝DF，∴DE＝2OF＝6．

∵OF＝3，BF＝2，∴OC＝OB＝5，CE＝10，

∴CD＝＝＝8，

由（1）知PE⊥CE．设PD＝x，则PC＝x+8．

在Rt△PDE和Rt△PCE中，由勾股定理，得：PD2+DE2＝PE2＝PC2-CE2，

即x2+62＝（x+8）2-102，

解得：x＝，

∴PD＝．

∴PE＝＝＝，

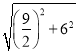∴PN＝PE＝．