题目内容
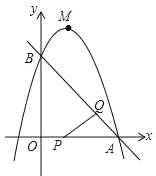
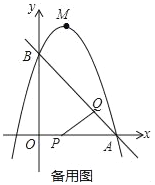
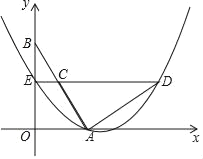
【题目】如图,两个完全相同的直角三角板放置在平面直角坐标系中,点A,B分别在x轴、y轴上,点C在边AB上,延长DC交y轴于点E.若点D的横坐标为5,∠OBA=30°,二次函数y=ax2+bx+c的图象经过点A,D,E,则a的值为_____.
【答案】![]()
【解析】
设A(m,0),根据含有30°角的直角三角板的特点,能够得到EC是△ABO的中位线,进而分别求出A,D,E三点的坐标,再将三点代入函数解析式,利用待定系数法求得a的值.
解:设A(m,0),
在Rt△ABO中,∠OBA=30°,
∴OB=![]() m,AB=2m,
m,AB=2m,
又∵△ACD是与△ABO相同的三角板,
∴∠ADC=30°,AC=m,CD=2m,
∴C是AB的中点,
又∵∠BEC=90°,
∴EC=![]() m,
m,
∴ED=![]() m,
m,
又∵ED=5,
∴m=2,
∴A(2,0),E(0,![]() ),D(5,
),D(5,![]() ),
),
∴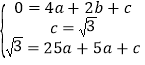 ,
,
∴a=![]() ,
,
故答案为:![]()

练习册系列答案
相关题目
【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?