��Ŀ����
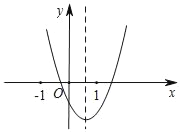
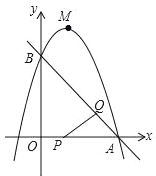
����Ŀ����ͼ����ֱ֪��y=��x+3��x�ᡢy��ֱ���A��B���㣬������y=��x2+bx+c����A��B���㣬��P���߶�OA�ϣ��ӵ�A��1����λ/����ٶ������˶���ͬʱ����Q���߶�AB�ϣ��ӵ�A���������B��![]() ����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ����APQΪֱ�������Σ�
��3������P��PE��y�ᣬ��AB�ڵ�E������Q��QF��y�ᣬ���������ڵ�F������EF����EF��PQʱ�����F�����꣮
���𰸡���1�������ߵĽ���ʽΪy=��x2+2x+3����2����t=1��t=![]() ʱ����PQA��ֱ�������Σ���3����F������Ϊ��2��3����
ʱ����PQA��ֱ�������Σ���3����F������Ϊ��2��3����
�������������������1��������ֱ�߽���ʽȷ��A���B�����꣬Ȼ�����ô���ϵ�����������ߵĽ���ʽ��
��2��OP=t��AQ=![]() t����PA=3-t�����жϡ�QAP=45�������ۣ�����PQA=90��ʱ����ͼ�٣����õ���ֱ�������ε����ʵ�PA=
t����PA=3-t�����жϡ�QAP=45�������ۣ�����PQA=90��ʱ����ͼ�٣����õ���ֱ�������ε����ʵ�PA=![]() AQ����3-t=
AQ����3-t=![]()
![]() t������APQ=90��ʱ����ͼ�������õ���ֱ�������ε����ʵ�AQ=
t������APQ=90��ʱ����ͼ�������õ���ֱ�������ε����ʵ�AQ=![]() AP����
AP����![]() t=
t=![]() ��3-t����Ȼ��ֱ�����t�ķ��̼��ɣ�
��3-t����Ȼ��ֱ�����t�ķ��̼��ɣ�
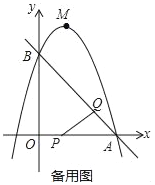
��3����ͼ�ۣ��ӳ�FQ��x���ڵ�H�����P������Ϊ��t��0�������E������Ϊ��t��-t+3��������AQHΪ����ֱ�������Σ���AH=HQ=![]() AQ=t����ɱ�ʾ����Q������Ϊ��3-t��t������F������Ϊ[3-t��-��3-t��2+2��3-t��+3��]������FQ=-t2+3t����֤���ı���PQFEΪƽ���ı��εõ�EP=FQ����3-t=3t-t2��Ȼ��ⷽ�����t���ɵõ���F������.
AQ=t����ɱ�ʾ����Q������Ϊ��3-t��t������F������Ϊ[3-t��-��3-t��2+2��3-t��+3��]������FQ=-t2+3t����֤���ı���PQFEΪƽ���ı��εõ�EP=FQ����3-t=3t-t2��Ȼ��ⷽ�����t���ɵõ���F������.
�����������1����y=��x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
�൱y=0ʱ��x=3����A������Ϊ��3��0������x=0ʱ��y=3����B������Ϊ��0��3����
�߽�A��3��0����B��0��3������ã� ![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��2����OA=OB=3����BOA=90����
���QAP=45����
��ͼ����ʾ����PQA=90��ʱ��

���˶�ʱ��Ϊt�룬��QA=![]() t��PA=3��t��
t��PA=3��t��
��Rt��PQA�� ![]() ����
����![]() ��
��
��ã�t=1��
��ͼ����ʾ����QPA=90��ʱ��

���˶�ʱ��Ϊt�룬��QA=![]() t��PA=3��t��
t��PA=3��t��
��Rt��PQA�� ![]() ����
����![]() ��
��
��ã�t=![]() ��
��
������������t=1��t=![]() ʱ����PQA��ֱ�������Σ�
ʱ����PQA��ֱ�������Σ�
��3����ͼ����ʾ��

���P��������t��0�������E��������t����t+3������EP=3��t����Q��������3��t��t������F��������3��t������3��t��2+2��3��t��+3������F��3��t��4t��t2������FQ=4t��t2��t=3t��t2��
��EP��FQ��EF��PQ��
���ı���EFQPΪƽ���ı��Σ�
��EP=FQ����3��t=3t��t2��
��ã�t1=1��t2=3����ȥ����
��t=1����õ�F������Ϊ��2��3����

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�����Ŀ��ij�̵��½�һ��̨�ƣ�����̨�Ƶijɱ���Ϊÿ��30Ԫ�������鷢�֣�����̨��ÿ���������y����λ�����������۵���x����λ��Ԫ����30��x��60����һ�κ�����
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
��1����������y�����۵���x֮��ĺ�������ʽ��
��2��������̨��ÿ�����������ΪwԪ������̨�����۵��۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��