��Ŀ����
����Ŀ�����壺��Q��ͼ��W��ÿһ����ľ������Сֵ��Ϊ��Q��ͼ��W�ľ��룮
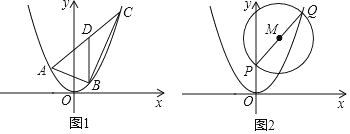
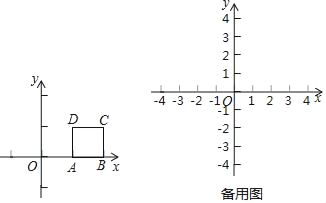
���磬��ͼ1��������ABCD����A��1��0����B��2��0����C��2��1����D��1��1������ô��O��0��0����������ABCD�ľ���Ϊ1��
��1�������P���ԣ�3��4��ΪԲ�ģ�2Ϊ�뾶��Բ����ô��O��0��0������P�ľ���Ϊ�� ����
��2�������M��3��0����ֱ����y��![]() x+4�ľ��룺
x+4�ľ��룺
�������N��0��a����ֱ��y��![]() x+4�ľ���Ϊ2����a��ֵ��
x+4�ľ���Ϊ2����a��ֵ��
��3�������G��0��b����������y��x2�ľ���Ϊ3����ֱ��д��b��ֵ��
���𰸡���1��3��2����![]() ��
��![]() ��
��![]() ��3����3��
��3����3��![]()
��������
���ݹ��ɶ����ɵõ�O��0��0���� P�ľ��룻
�ٹ���M��M��M��l������Ϊ��M�䣬��ֱ�������ε����ʿɵ�M��M��MA sin��M��AM��6��![]() ��
��![]() ���Ӷ��õ���M��ֱ��
���Ӷ��õ���M��ֱ��![]() �ľ��룻
�ľ��룻
�ڷ����������N��l���ϱߣ�N��l���±ߣ����������ȵõ�BN�ij�����һ�����ɵõ�a��ֵ��
������������ٵ�G��ԭ�����棻�ڵ�G��ԭ�����棻�������ۼ��ɵõ�b��ֵ��
��1������OP��Բ�ڵ�Q��

������ã�OQΪ��O��0��0������P�ľ��룬
��P��3��4����OP��5����PQ��5��2��3��
�ʴ���3��
��2��������ͼ��ʾ���裺ֱ��Ϊl�ķ���Ϊ��y��![]() x+4��
x+4��
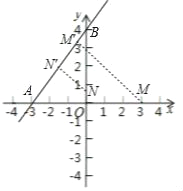
ֱ����x�ᡢy�ύ�������ֱ�Ϊ����3��0������0��4����tan��M��AM��![]() ��
��
����M��M��M��ֱ��l����M��MΪM��ֱ��l�ľ��룬
M��M��MA sin��M��AM��6��![]() ��
��![]() ��
��
��������ã���N��ֱ��l�·�ʱ��
N��N��2��BN��![]() ��
��![]() ��
��
��a��4��![]() ��
��![]() ��
��
��N��ֱ��l�Ϸ�ʱ��a����a��4+ ![]() ��
��![]() ��
��
��a��![]() ��
��![]() ��
��
��3����G��ԭ���·�ʱ��b����3��
��G��ԭ���Ϸ�ʱ��![]() ��
��
�����ã�x4+��1��2b��x2+b2��9��0��
������1��2b��2��4��b2��9����0��
��ã�b��![]() ��
��
��b����3��![]() ��
��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�