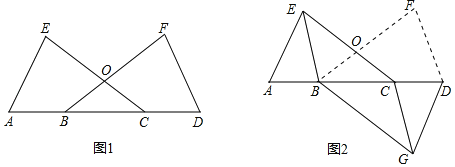题目内容
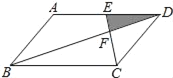
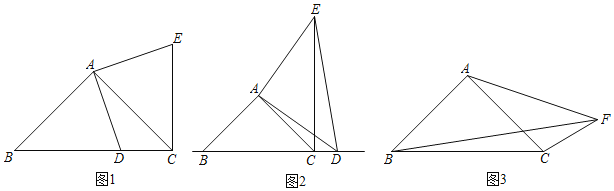
【题目】（1）问题发现：如图1，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是 ，位置关系是 ；
（2）探究证明：如图2，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC的延长线上时，连接EC，写出此时线段AD，BD，CD之间的等量关系，并证明；
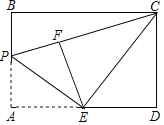
（3）拓展延仲：如图3，在四边形ABCF中，∠ABC＝∠ACB＝∠AFC＝45°．若BF＝13，CF＝5，请直接写出AF的长．
【答案】（1）BD＝CE，BD⊥CE；（2）2AD2＝BD2+CD2，理由详见解析；（3）
.
【解析】
（1）证明△BAD≌△CAE，根据全等三角形的性质解答；
（2）证明△BAD≌△CAE，得到BD=CE，根据勾股定理计算即可；
（3）如图3，作辅助线，构建全等三角形，证明△BAF≌△CAG，得到CG＝BF＝13，证明
是直角三角形，根据勾股定理计算即可.
解：（1）在Rt△ABC中，AB＝AC，
∴∠B＝∠ACB＝90°，
∵∠BAC＝∠DAE＝90°，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，
在△BAD和△CAE中，
∵
，
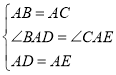∴△BAD≌△CAE（SAS），
∴BD＝CE，∠B＝∠ACE＝45°，
∵∠ACB＝45°，
∴
，
故答案为：BD＝CE，BD⊥CE；
（2）2AD2＝BD2+CD2，理由是：如图2，
∵∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
在△ABD和△ACE中，
∵，
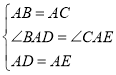∵△BAD≌△CAE（SAS），
∴BD＝CE，∠B＝∠ACE＝45°，
∴∠BCE＝∠ACB+∠ACE＝45°+45°＝90°，
∴DE2＝CE2+CD2，
∵AD＝AE，∠DAE＝90°，
∴
，
∴2AD2＝BD2+CD2；
（3）如图3，将AF绕点A逆时针旋转90°至AG，连接CG、FG，
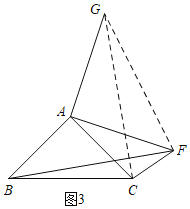
则△FAG是等腰直角三角形，
∴∠AFG＝45°，
∵∠AFC＝45°，
∴∠GFC＝90°，
同理得：△BAF≌△CAG，
∴CG＝BF＝13，
Rt△CGF中，∵CF＝5，
∴FG＝12，
∵△FAG是等腰直角三角形，
∴
．
